Hyperbel
Unter einer Hyperbel versteht man den Graph einer gebrochenrationalen Funktion des Typs f(x) = 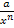 mit a
mit a  ℝ\
ℝ\ 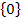 , n
, n  ℕ
ℕ
(a ist eine Konstante, die alle dir bekannten Zahlen außer Null annehmen kann, wogegen der Exponent n zwar auch konstant ist, aber nur natürliche Zahlen, d.h. ganze positive Zahlen, annehmen darf.)
Die einfachste Hyperbel ist der Graph der Funktion f(x) =  . Siehe Abbildung!
. Siehe Abbildung!
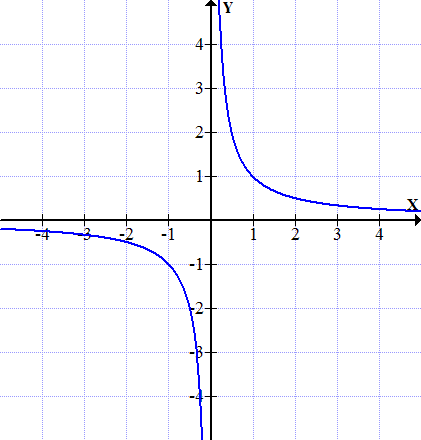
Graph der Funktion f(x) = 
Auf Hyperbeln stößt man beispielsweise im Zusammenhang mit der indirekten Proportionalität. Allerdings ist der Exponent dabei stets n = 1. Die Abbildungsvorschrift der indirekten Proportionalität lautet nämlich f:x 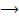
 oder anders, nämlich als Funktionsterm geschrieben, f(x) =
oder anders, nämlich als Funktionsterm geschrieben, f(x) =  und das ergibt gezeichnet natürlich eine Hyperbel.
und das ergibt gezeichnet natürlich eine Hyperbel.
Das Besondere an Hyperbeln sind ihre Asymptoten (= Geraden, an die sich der Graph anschmiegt). Eine Hyperbel hat immer sowohl eine waagrechte als auch eine senkrechte Asymptote.
Die Funktion f(x) =  hat die x-Achse als waagrechte Asymptote und die y-Achse als senkrechte Asymptote. Die senkrechte Asymptote liegt immer bei der Definitionslücke der Funktion. Die Funktion f(x) =
hat die x-Achse als waagrechte Asymptote und die y-Achse als senkrechte Asymptote. Die senkrechte Asymptote liegt immer bei der Definitionslücke der Funktion. Die Funktion f(x) =  hat beispielsweise die Definitionslücke x = 0, da der Nenner Null ergeben würde, wenn man für x die Zahl Null einsetzte;die Division durch Null ist aber nicht definiert. Man kann also für x bei dieser Funktion nicht Null einsetzen. Allerdings können für x Werte gewählt werden, die vom Betrag her sehr klein sind, die sich also an Null beliebig nah annähern. Dabei ergeben sich Funktionswerte f(x) bzw. y, welche vom Betrag her sehr großsind. 1 geteilt durch eine Zahl, die fast Null ist (z. B. x = 0,01 oder x = 0,001) ergibt schließlich etwas sehr Großes (z.B. f(0,01) =
hat beispielsweise die Definitionslücke x = 0, da der Nenner Null ergeben würde, wenn man für x die Zahl Null einsetzte;die Division durch Null ist aber nicht definiert. Man kann also für x bei dieser Funktion nicht Null einsetzen. Allerdings können für x Werte gewählt werden, die vom Betrag her sehr klein sind, die sich also an Null beliebig nah annähern. Dabei ergeben sich Funktionswerte f(x) bzw. y, welche vom Betrag her sehr großsind. 1 geteilt durch eine Zahl, die fast Null ist (z. B. x = 0,01 oder x = 0,001) ergibt schließlich etwas sehr Großes (z.B. f(0,01) = 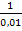 =100 oder f(0,001) =
=100 oder f(0,001) = 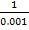 = 1000). Zeichnet man diese Punkte und noch viele weitere mit einer x-Koordinate, die fast Null ist, in ein Koordinatensystem ein, erkennt man:Der Graph der Funktion f(x) =
= 1000). Zeichnet man diese Punkte und noch viele weitere mit einer x-Koordinate, die fast Null ist, in ein Koordinatensystem ein, erkennt man:Der Graph der Funktion f(x) =  schmiegt sich an die Gerade x = 0 (das ist die Gleichung der y-Achse) beliebig nah an. Die Gleichung x = 0 ist deshalb die Gleichung der senkrechten Asymptote. Die Funktion f(x) =
schmiegt sich an die Gerade x = 0 (das ist die Gleichung der y-Achse) beliebig nah an. Die Gleichung x = 0 ist deshalb die Gleichung der senkrechten Asymptote. Die Funktion f(x) =  hat die y-Achse als senkrechte Asymptote.
hat die y-Achse als senkrechte Asymptote.
Wie erhält man nun aber die Gleichung der waagrechten Asymptote? An die waagrechte Asymptote schmiegt sich die Hyperbel im Koordinatensystem ganz weit links und ganz weit rechts an, also für vom Betrag her sehr große x-Werte. Setzt man deshalb jetzt für x in die Funktionsgleichung f(x) =  betragsmäßig sehr große Zahlen ein (z.B. x = 100 oder x = 1000), erhält man Funktionswerte f(x) bzw. y, die vom Betrage her sehr klein sind (z.B. f(100) = 0.01 oder f(1000) = 0,001). Dennoch wird sich niemals für f(x) bzw. y genau der Wert Null ergeben. Die Funktion nähert sich zwar an y = 0 an, erreicht den Wert y = 0 aber nicht. Die Gleichung y = 0 beschreibt daher die waagrechte Asymptote. Da y = 0 auch die Gleichung der x-Achse ist, ist die x-Achse die waagrechte Asymptote der Funktion f(x) =
betragsmäßig sehr große Zahlen ein (z.B. x = 100 oder x = 1000), erhält man Funktionswerte f(x) bzw. y, die vom Betrage her sehr klein sind (z.B. f(100) = 0.01 oder f(1000) = 0,001). Dennoch wird sich niemals für f(x) bzw. y genau der Wert Null ergeben. Die Funktion nähert sich zwar an y = 0 an, erreicht den Wert y = 0 aber nicht. Die Gleichung y = 0 beschreibt daher die waagrechte Asymptote. Da y = 0 auch die Gleichung der x-Achse ist, ist die x-Achse die waagrechte Asymptote der Funktion f(x) =  .
.
Entsprechendes gilt für alle Funktionen des Typs f(x) = 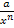 . Beispielsweise hat auch die Funktion f(x) =
. Beispielsweise hat auch die Funktion f(x) = 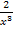 die x-Achse als waagrechte und die y-Achse als senkrechte Asymptote.
die x-Achse als waagrechte und die y-Achse als senkrechte Asymptote.
|
Merke: Alle Funktionen des Typs f(x) = |
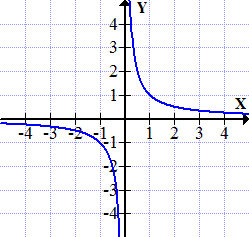
Wichtig für das Aussehen einer Hyperbel ist vor allem die Potenz n in der Funktionsgleichung f(x) = 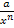 . Entscheidend dabei ist, ob n eine gerade oder ungerade Zahl ist. Alle Hyperbeln mit ungeraden Exponenten ähneln dem bereits oben gezeigten Graphen der Funktion f(x) =
. Entscheidend dabei ist, ob n eine gerade oder ungerade Zahl ist. Alle Hyperbeln mit ungeraden Exponenten ähneln dem bereits oben gezeigten Graphen der Funktion f(x) =  . Daher sind Hyperbeln f(x) =
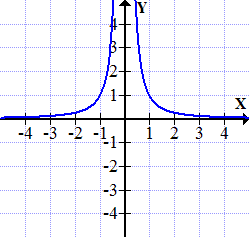
. Daher sind Hyperbeln f(x) = 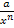 mit ungeradem Exponenten punktsymmetrisch zum Ursprung. Alle Hyperbeln mit geraden Exponenten ähneln dagegen dem Graph der Funktion f(x) =
mit ungeradem Exponenten punktsymmetrisch zum Ursprung. Alle Hyperbeln mit geraden Exponenten ähneln dagegen dem Graph der Funktion f(x) = 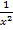 . Deshalb sind Hyperbeln f(x) =
. Deshalb sind Hyperbeln f(x) = 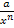 mit geraden Exponenten achsensymmetrisch zur y-Achse.
mit geraden Exponenten achsensymmetrisch zur y-Achse.
 |
 |
Graph der Funktion f(x) =  |
Graph der Funktion f(x) = 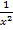 |
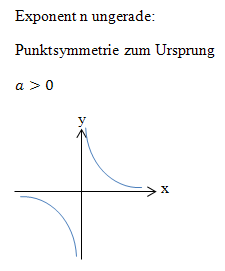
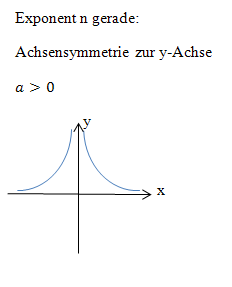
Außerdem ist das Vorzeichen des Koeffizienten a in der Funktionsgleichung f(x) = 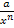 wichtig. (Damit ist das Vorzeichen des Zählers oder auch des ganzen Bruchs gemeint.) Ist dieses Vorzeichen positiv und die Funktion hat einen ungeraden Exponenten, verläuft die Hyperbel im I:und III. Quadranten. Vergleiche Abbildung oben links! Bei positivem Vorzeichen von a, aber geradem Exponenten n verläuft die Hyperbel im I. und II. Quadranten. Vergleiche Abbildung oben rechts! Ist das Vorzeichen von a dagegen negativ, ergibt sich ein an der x-Achse gespiegelter Graph. Bei ungeradem Exponenten liegt die Hyperbel dann im II. und IV. Quadranten. Bei geradem Exponenten liegt die Hyperbel dann im III. und IV. Quadranten.
wichtig. (Damit ist das Vorzeichen des Zählers oder auch des ganzen Bruchs gemeint.) Ist dieses Vorzeichen positiv und die Funktion hat einen ungeraden Exponenten, verläuft die Hyperbel im I:und III. Quadranten. Vergleiche Abbildung oben links! Bei positivem Vorzeichen von a, aber geradem Exponenten n verläuft die Hyperbel im I. und II. Quadranten. Vergleiche Abbildung oben rechts! Ist das Vorzeichen von a dagegen negativ, ergibt sich ein an der x-Achse gespiegelter Graph. Bei ungeradem Exponenten liegt die Hyperbel dann im II. und IV. Quadranten. Bei geradem Exponenten liegt die Hyperbel dann im III. und IV. Quadranten.
Übersicht:
 |
 |
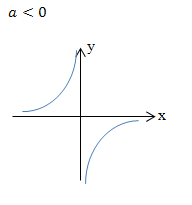 |
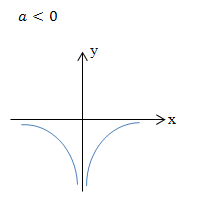 |
Hyperbeln können auch zur Seite und nach oben oder unten verschoben sein. Die Funktionsgleichung einer verschobenen Hyperbel lautet allgemein:
f(x) = 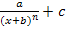 mit n
mit n  ℕ , a
ℕ , a 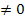
Der Graph so einer Hyperbel entsteht durch Verschiebung der entsprechenden Hyperbel y = 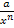 um b nach links (b
um b nach links (b 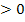 ) bzw. nach rechts (b
) bzw. nach rechts (b 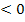 ) und um c nach oben (c
) und um c nach oben (c 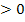 ) bzw. nach unten (c
) bzw. nach unten (c 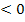 ). Daher gilt für die Gleichungen der Asymptoten:
). Daher gilt für die Gleichungen der Asymptoten:
Senkrechte Asymptote: x = -b
Waagrechte Asymptote: y = c
Wenn Exponent n ungerade:Punktsymmetrie zum Punkt P(-b|c)
Wenn Exponent n gerade: Achsensymmetrie zur Achse x = -b
Beispiel:
f(x) = 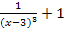
Definitionsmenge: Bis 8. Klasse: 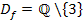
![]() Ab 9.Klasse:
Ab 9.Klasse: 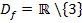
Wertemenge:![]() Bis 8. Klasse:
Bis 8. Klasse: 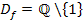
![]() Ab 9.Klasse:
Ab 9.Klasse: 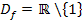
Senkrechte Asymptote: x = 3
Waagrechte Asymptote: y = 1
Symmetrie: Exponent n = 3 (ungerade)  Punktsymmetrie zum Punkt P(3|1)
Punktsymmetrie zum Punkt P(3|1)
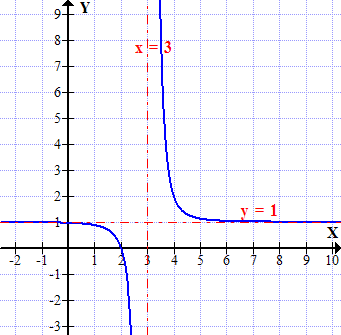
Graph der Funktion f(x) = 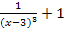 mit seinen Asymptoten
mit seinen Asymptoten
Mehr zum Thema Hyperbel findest du im Bereich Analysis im Kapitel Gebrochenrationale Funktionen.

