Minimum

Unter einem absoluten oder globalen Minimum einer Funktion versteht man genau genommen den absolut kleinsten Funktionswert, den eine Funktion annehmen kann. Der zugehörige Punkt auf dem Graph der Funktion heißt absoluter Tiefpunkt. Oft werden die Begriffe Tiefpunkt und Maximum jedoch gleichbedeutend verwendet.

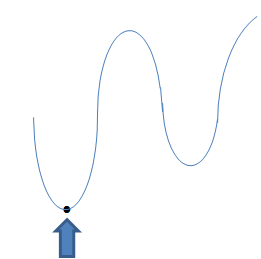
Absoluter Tiefpunkt (absolut tiefster Punkt des gesamten Graphen)

Von den absoluten Minima sind die relativen Minima zu unterscheiden. Beide zählen neben den Maxima zu den Extrema einer Funktion. Siehe auch:Extremum

Ein relatives Minimum, auch lokales Minimum genannt, liegt vor, wenn es sich nicht um den absolut kleinsten y-Wert handelt, sondern nur um den kleinsten Funktionswert innerhalb einer bestimmten Umgebung. Der zugehörige Punkt auf dem Funktionsgraph heißt relativer oder auch lokaler Tiefpunkt. Ein relativer Tiefpunkt liegt also nur innerhalb einer bestimmten Umgebung am tiefsten, ist aber nicht der am allertiefsten gelegene Punkt insgesamt.

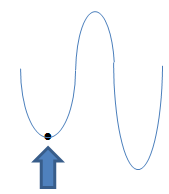
Relativer Tiefpunkt (nicht absolut tiefster Punkt des ganzen Graphen, sondern nur in dieser Umgebung)

Berechnung der Minima einer Funktion f(x):

Da die Tangente an den Funktionsgraph bei einem Minimum waagrecht verläuft, muss die Tangentensteigung und somit auch die Steigung der Funktion an dieser Stelle gleich Null sein. Die Steigung einer Funktion berechnet man mit ihrer ersten Ableitung f´(x). Daher gilt:

f´(x) = 0

Dadurch werden die x-Koordinaten aller Punkte mit waagrechten Tangenten, also der Minima, aber auch der Maxima und Terrassenpunkte, berechnet. Der Nachweis, dass wirklich ein Minimum vorliegt, gelingt entweder durch die Untersuchung der Monotonie der Funktion oder mit Hilfe der zweiten Ableitung.

Nachweis eines (relativen) Minimums mit Hilfe der Monotonie:

Wenn der Graph zuerst fällt (negative Steigung f´(x)) und dann steigt (positive Steigung f´(x)), liegt ein (relatives) Minimum vor und der Graph hat dort einen relativen Tiefpunkt, kurz TIP. Ob es sich sogar um ein absolutes Minimum handelt, kann man erst am Verlauf des gesamten Graphen beurteilen. Gibt es jedoch nur eine einzige Monotonieänderung, liegt auf jeden Fall ein absolutes Extremum vor.

Monotonietabelle:

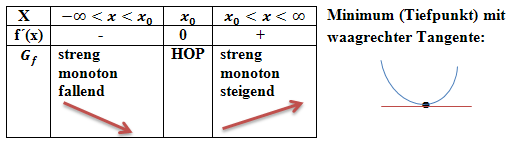
Nachweis eines (relativen) Minimums mit Hilfe der zweiten Ableitung:

In der 12. Klasse lernst du die zweite Ableitung f´´(x) kennen, welche die Krümmung der Funktion f(x) beschreibt. Ist die zweite Ableitung f´´(x) positiv, ist der Graph linksgekrümmt;ist f´´(x) dagegen negativ, ist der Graph rechtsgekrümmt.

Da der Graph in der Umgebung eines Minimums stets linksgekrümmt ist, muss im Falle des Vorliegens eines Minimums an der Stelle 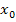gelten:

f´´( 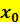) 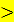0

Einfacher gesagt:Man setzt die mit dem Ansatz f´(x) = 0 ermittelte x-Koordinate 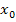in die zweite Ableitung f´´(x) ein;ergibt sich dabei ein positiver Wert, liegt ein relatives Minimum vor. Ob es sich sogar um ein absolutes Minimum handelt, kann man nur am Verlauf des gesamten Graphen beurteilen.

Die y-Koordinate des Minimums erhält man, wenn man die x-Koordinate des Minimums 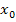in die Funktionsgleichung f(x) einsetzt. Vorsicht:Nicht in die Ableitung einsetzen, wenn man y ermitteln will, sonst würden wir die Steigung an dieser Stelle erhalten und nicht den Funktionswert y!

y = f( )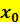

Konkrete Beispiele zur Berechnung der Minima einer Funktion und noch weitere Informationen zu diesem Thema findest du im Bereich Analysis in den Kapiteln Erste Ableitung f´(x) bzw. Zweite Ableitung f´´(x) und Kurvendiskussion.