Parabelscharen

) Einfacher wäre es sicher, wenn der Scharparameter nicht gerade 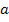, sondern z.B. k oder r hieße. Nun wirst du dich vielleicht fragen, warum in diesem Aufgabenbeispiel für den Scharparameter überhaupt die Bezeichnung 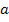gewählt wurde. Wäre der Scharparameter beispielsweise einfach k oder r genannt worden, hätten wir dieses Problem schließlich gar nicht. Gerade dieser „Haken“ sollte hier jedoch aufgezeigt werden, denn in anderen Aufgaben wirst du vielleicht irgendwann einmal vor dem gleichen Problem stehen. So, nun bilden wir endlich unsere Diskriminante:

=

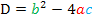
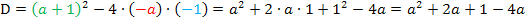
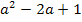
Erfreulicherweise lässt sich der Ausdruck 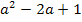mit Hilfe der zweiten binomischen Formel 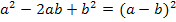noch weiter umformen. So erhalten wir:

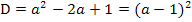
Dass die letzte Umformung mit der binomischen Formel möglich war, ist für uns sehr hilfreich. Es vereinfacht die Aufgabe deutlich, weil dadurch ein Ausdruck mit Quadrat (insgesamt) entstanden ist, und man kann nun sofort erkennen, dass die Diskriminante D in diesem Fall nicht negativ werden kann. Egal, was für 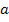eingesetzt wird, also unabhängig von 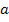, wird D niemals negativ, da ein Quadrat nicht negativ werden kann. Die Diskriminante D kann hier entweder gleich Null sein, dann gibt es genau eine Lösung, d.h. einen Berührpunkt, oder zwei verschiedene Lösungen, d.h. zwei Schnittpunkte. Diese beiden Fälle müssen wir nun unterscheiden. Wir müssen also überlegen, was für 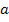eingesetzt werden kann, damit die Diskriminante gleich Null wird, und für welche Werte von 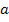die Diskriminante positiv wird.

1. Fall: D = 0

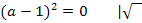
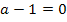
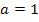
Für 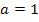ergibt sich D = 0 und somit hat nur die Scharparabel 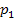genau einen gemeinsamen Punkt mit der Winkelhalbierenden des II. und IV. Quadranten, also mit der Gerade 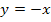. Die Winkelhalbierende 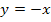ist daher Tangente an die Scharparabel .

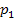2. Fall: D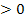

Der zweite Fall ergibt sich ohne große Rechnung als logische Konsequenz des ersten. Die Diskriminante D soll positiv werden. Das ist genau dann der Fall, wenn 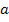nicht gleich 1 ist. Für 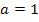würde D = 0 sein, aber wir suchen nun gerade nach allen Werten von 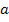, für die D größer als Null wird. (Einen dritten Fall, nämlich D 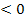gibt es hier ja nicht, da der Ausdruck 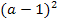wegen des Quadrates nicht negativ sein kann!) Damit D positiv wird, darf der Scharparameter 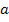also alle Werte ausschließlich 1 annehmen. Dann existieren zwei Schnittpunkte der Scharparabel 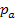und der Winkelhalbierenden des II. und IV. Quadranten. Die Winkelhalbierende 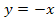ist also Sekante aller Scharparabeln außer für .

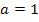D

---