Gleichungen mit lnx oder e^x lösen, einschließlich ln-Rechengesetze

Wenn du bei ln-Funktionen die ln-Rechengesetze anwendest, immer kontrollieren, ob die Definitionsmenge unverändert bleibt! Nur wenn sich an der Definitionsmenge nichts ändert, darfst du die ln-Rechengesetze anwenden!

Bsp.: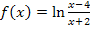

Bei dieser Funktion könnte man auf die Idee kommen, folgende Umformung mit dem zweiten ln-Rechengesetz 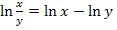zu machen:

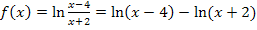
Dadurch würde sich die Funktion beispielsweise wesentlich leichter ableiten lassen. Aber Vorsicht:Dann verändert sich die Definitionsmenge!

Betrachten wir die Funktion 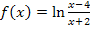und die Funktion .

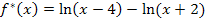Ermitteln wir doch mal die Definitionsmengen beider Funktionen und vergleichen sie miteinander!

Definitionsmenge von 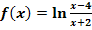ermitteln:

Das Argument des ln, also hier der Bruch, muss positiv sein;ansonsten ist der ln nicht definiert. Daher müssen wir die folgende Ungleichung lösen:

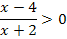
Wie löst man nun diese Bruch-Ungleichung? Hast du eine Idee?

Wie du weißt, ist ein Bruch positiv, wenn entweder Zähler und Nenner beide positiv sind oder wenn beide negativ sind.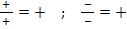

Deshalb müssen wir die folgenden zwei Fälle unterscheiden:

1. Fall:Zähler >0 und Nenner >0  oder  2. Fall:Zähler <0 und Nenner <0

Auf unsere Bruch-Ungleichung bezogen, heißt das:

Wir markieren uns in beiden Fällen jeweils die Bereiche am Zahlenstrahl.

Zum 1. Fall:Größer als 4 bedeutet von 4 nach rechts am Zahlenstrahl;größer als -2 entsprechend von -2 nach rechts. (Die Zahlen 4 und -2 sind dabei jeweils ausgeschlossen.) Zum 2. Fall:Kleiner als 4 bedeutet umgekehrt von 4 nach links;kleiner als -2 entsprechend von -2 nach links. (Die Zahlen 4 und -2 sind dabei jeweils ausgeschlossen.)

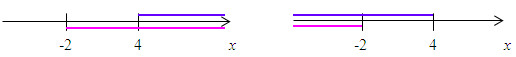
Wir brauchen bei beiden Fällen jeweils den Bereich, der am Zahlenstrahl sowohl blau als auch rosa markiert ist, denn es sollen jeweils die blau unterstrichene und die rosa unterstrichene Ungleichung zugleich erfüllt sein. Wir nehmen also jeweils den Bereich, der blau und rosa markiert ist.

Aus dem 1. Fall ergibt sich: 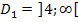Aus dem 2. Fall ergibt sich: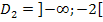

Die zulässigen x-Werte liegen also entweder in 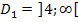oder in 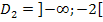. Die gesamte Definitionsmenge 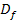erhalten wir, indem wir 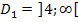mit 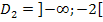vereinigen.

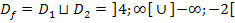
Schöner geschrieben:

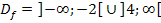
Man darf also die Zahlen von einschließlich -2 bis einschließlich 4 nicht einsetzen. Man kann daher auch schreiben:

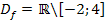
Die Zahlen -2 und 4 dürfen nicht eingesetzt werden, daher muss man sie beide ausschließen. Deshalb sind die eckigen Klammer bei 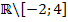zu der -2 und 4 hin gerichtet. Die beiden Zahlen soll noch mitausgeschlossen werden.

---