Kurzwiederholung des Logarithmus (zur allgemeinen Basis a) inklusive log-Rechengesetze
)
Gesucht: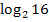 
Wir stellen die zugehörige Exponentialgleichung auf, d.h. wir fragen uns:„2 hoch was ergibt 16?“
Zu lösen ist also die Gleichung:
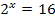
Nun versuchen wir die Zahl 16 als Potenz der Zahl 2 zu schreiben. Du überlegst dir dazu, wie oft du die Zahl 2 mit sich selbst multiplizieren musst, um auf 16 zu kommen. Überlegung:
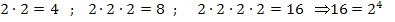
Nun wissen wir die Lösung eigentlich schon: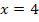 
und somit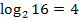 
Noch einmal ganz ausführlich geschrieben:
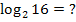
Zugehörige Exponentialgleichung:
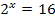
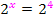
Den letzten Schritt nennt man übrigens Exponentenvergleich. Wenn die Basis auf beiden Seiten der Gleichung dieselbe Zahl (hier 2) ist, muss auch der Exponent gleich sein. Deshalb muss gelten: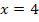
Daraus folgt: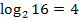
Kontrolle: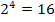 
Zu 1b.)
Gesucht: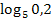 
Wir stellen die zugehörige Exponentialgleichung auf, d.h. wir fragen uns:„5 hoch was ergibt 0,2?“
Zu lösen ist also die Gleichung:
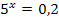
Nun versuchen wir die Zahl 0,2 als Potenz der Zahl 5 zu schreiben. Dazu schreiben wir 0,2 vorab als Bruch: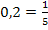 
Mit Hilfe des Potenzgesetzes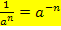 
lässt sich 
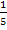bequem als Potenz der Zahl 5 schreiben. Es gilt schließlich: 
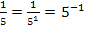Damit ergibt sich:
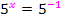
Der Exponentenvergleich liefert die Lösung:
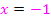
Daraus folgt: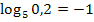 
Zu 1c.)
Gesucht: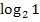 
Wir fragen uns also:„2 hoch was ergibt 1?“ D.h. wir müssen die folgende Exponentialgleichung lösen:
Wie lässt sich nun aber die Zahl 1 als Potenz der Zahl 2 schreiben?
Bitte erst mal selbst nachdenken!
Erinnerst du dich noch daran, dass jede beliebige Zahl hoch Null genommen die Zahl 1 ergibt? Es gilt also auch: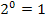 
Damit ist die Lösung klar:x = 0
Es folgt somit: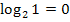 
Merke:Ist das Argument (d.h. die Zahl direkt hinter dem Logarithmus;also die Zahl, auf die sich der Logarithmus bezieht) die 1, dann ergibt sich für jede beliebige Basis das Ergebnis 0. Denn aus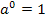 
folgt allgemein für a >0 und 
:
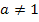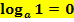
Z.B.: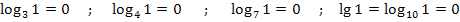 
Zu 1d.)
Gesucht: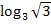 
Zugehörige Exponentialgleichung:
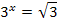
Die Wurzel schreiben wir als Potenz. Zur Erinnerung: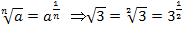 
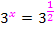
Exponentenvergleich liefert:
Daraus folgt: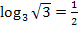 
Zu 1e.)
Gesucht: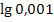 
Statt 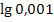könnte man auch ausführlich 
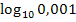schreiben, da lg nur die Abkürzung für den Zehner-Logarithmus ist. Wir müssen uns also fragen:„10 hoch was ergibt 0,001?“ Die zugehörige Exponentialgleichung lautet somit:
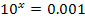
Die Zahl 0,001 schreiben wir als Bruch.
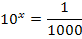
Wir müssen auch auf der rechten Seite der Gleichung letztendlich auf die Basis 10 kommen, damit wir nachher einen Exponentenvergleich machen können.
