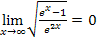Grenzwerte von e- und ln-Funktionen
Geg.: 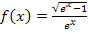
Ges.: 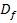 und Verhalten für
und Verhalten für  (einschließlich der Asymptote)
(einschließlich der Asymptote)
Ermittlung der maximalen Definitionsmenge 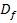 :
:
Der Nenner der Funktion macht uns keine Probleme. Bei 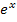 kann man alle reellen Zahlen einsetzen, weil
kann man alle reellen Zahlen einsetzen, weil 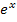 für x
für x  ℝdefiniert ist. Da
ℝdefiniert ist. Da 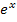 sowieso immer positiv ist, egal was man für x einsetzt, kann der Nenner in diesem Fall niemals gleich Null werden. In den Nenner kann man also sämtliche reelle Zahlen einsetzen. Anders sieht es jedoch mit dem Zähler der Funktion aus. Der Ausdruck
sowieso immer positiv ist, egal was man für x einsetzt, kann der Nenner in diesem Fall niemals gleich Null werden. In den Nenner kann man also sämtliche reelle Zahlen einsetzen. Anders sieht es jedoch mit dem Zähler der Funktion aus. Der Ausdruck 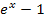 , der im Zähler unter der Wurzel steht, muss schließlich größer oder gleich Null sein;ansonsten wäre die Wurzel nicht definiert. Dass der Radikand, d.h. der Ausdruck unter der Wurzel, nicht negativ sein darf, ist dir bestimmt klar:Aus negativen Zahlen kann man die Wurzel ja nicht ziehen. Die Funktion ist also nur dann definiert, wenn gilt:
, der im Zähler unter der Wurzel steht, muss schließlich größer oder gleich Null sein;ansonsten wäre die Wurzel nicht definiert. Dass der Radikand, d.h. der Ausdruck unter der Wurzel, nicht negativ sein darf, ist dir bestimmt klar:Aus negativen Zahlen kann man die Wurzel ja nicht ziehen. Die Funktion ist also nur dann definiert, wenn gilt:
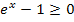
Um herauszufinden, für welche x diese Ungleichung erfüllt ist, lösen wir einfach nach x auf.
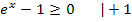

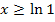
![]()
Die gesuchte Definitionsmenge lautet daher: 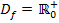
Verhalten von 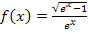 für
für  :
:
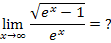
Setzt man in Gedanken Unendlich für x ein, stellt man fest, dass sowohl der Zähler als auch der Nenner von 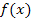 gegen Unendlich gehen. Es gilt schließlich:
gegen Unendlich gehen. Es gilt schließlich: 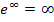 Wir stehen also vor dem Problem
Wir stehen also vor dem Problem  , was bekanntlich ein unbestimmter Ausdruck ist. Damit wir den Grenzwert leichter berechnen können, formen wir
, was bekanntlich ein unbestimmter Ausdruck ist. Damit wir den Grenzwert leichter berechnen können, formen wir 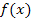 so um, dass die Wurzel über dem gesamten Bruch zu stehen kommt. Es soll also nachher alles unter einer großen Wurzel stehen. Dazu muss der Nenner quadriert werden.
so um, dass die Wurzel über dem gesamten Bruch zu stehen kommt. Es soll also nachher alles unter einer großen Wurzel stehen. Dazu muss der Nenner quadriert werden.
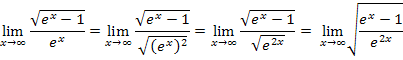
Hinweis:Bei der Umformung 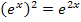 wurde das Potenzgesetz
wurde das Potenzgesetz 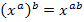 verwendet.
verwendet.
Als nächstes teilen wir den Bruch unter der Wurzel in zwei Einzelbrüche auf. Jeder Summand im Zähler wird dazu einzeln durch den Nenner 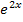 geteilt. Beim ersten Teilbruch lässt sich dann mit
geteilt. Beim ersten Teilbruch lässt sich dann mit 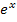 kürzen.
kürzen.
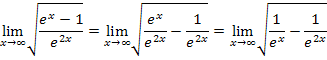
Die Grenzwerte von 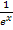 und
und 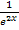 für
für  lassen sich leicht ermitteln. Es gilt:
lassen sich leicht ermitteln. Es gilt:
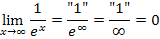
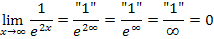
Damit lässt sich der gesuchte Grenzwert leicht ausrechnen.
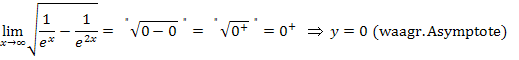
(Es ergibt sich 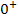 , weil das Ergebnis einer Wurzel immer positiv ist, wenn die Zahl unter der Wurzel nicht exakt gleich Null ist.)
, weil das Ergebnis einer Wurzel immer positiv ist, wenn die Zahl unter der Wurzel nicht exakt gleich Null ist.)
Die Funktion 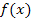 hat für
hat für  die x-Achse als waagrechte Asymptote. Am Vorzeichen von
die x-Achse als waagrechte Asymptote. Am Vorzeichen von 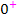 erkennt man, dass sich der Graph
erkennt man, dass sich der Graph 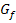 für
für  von oben an die x-Achse annähert.
von oben an die x-Achse annähert.
Alternativ zu der soeben gezeigten Berechnung des Grenzwertes 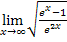 durch Aufteilen des Bruches in zwei Einzelbrüche, kann man auch folgendermaßen argumentieren:
durch Aufteilen des Bruches in zwei Einzelbrüche, kann man auch folgendermaßen argumentieren:
Der Bruch 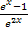 geht gegen Null, weil der Nenner schneller wächst als der Zähler. (
geht gegen Null, weil der Nenner schneller wächst als der Zähler. ( 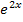 und
und 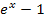 gehen beide gegen Unendlich, aber der Nenner
gehen beide gegen Unendlich, aber der Nenner 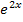 geht schneller gegen Unendlich als der Zähler
geht schneller gegen Unendlich als der Zähler 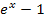 . „Kleineres Unendlich“ durch „größeres Unendlich“ geht gegen Null.) Die Wurzel aus Null ergibt wieder Null, also gilt:
. „Kleineres Unendlich“ durch „größeres Unendlich“ geht gegen Null.) Die Wurzel aus Null ergibt wieder Null, also gilt: