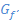Art der Extrema mit 2. Ableitung zu 8. Bsp.
Die zweite Ableitung 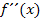 beschreibt die relative Veränderung der Steigung des Funktionsgraphen
beschreibt die relative Veränderung der Steigung des Funktionsgraphen  . Dies entspricht der Krümmung des Graphen
. Dies entspricht der Krümmung des Graphen  .
.
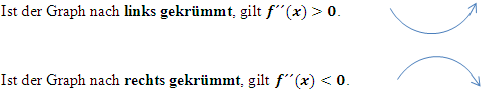
Mit Hilfe der zweiten Ableitung 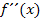 lässt sich ganz schnell herausfinden, ob ein Punkt mit waagrechter Tangente ein Hoch-, Tief- oder Terrassenpunkt ist. Man muss nur die entsprechende x-Koordinate des zu untersuchenden Punktes mit waagrechter Tangente in die zweite Ableitung
lässt sich ganz schnell herausfinden, ob ein Punkt mit waagrechter Tangente ein Hoch-, Tief- oder Terrassenpunkt ist. Man muss nur die entsprechende x-Koordinate des zu untersuchenden Punktes mit waagrechter Tangente in die zweite Ableitung 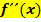 einsetzen. Ergibt sich dabei ein positives Ergebnis, liegt ein Tiefpunkt (TIP) vor;ergibt sich ein negatives Ergebnis, liegt ein Hochpunkt (HOP) vor. Das wird dir bestimmt sofort klar, wenn du dir die beiden Skizzen unten links anschaust.
einsetzen. Ergibt sich dabei ein positives Ergebnis, liegt ein Tiefpunkt (TIP) vor;ergibt sich ein negatives Ergebnis, liegt ein Hochpunkt (HOP) vor. Das wird dir bestimmt sofort klar, wenn du dir die beiden Skizzen unten links anschaust.
Bei einem TIPmuss der Graph eine waagrechte Tangente besitzen und links gekrümmt sein und daher gilt: 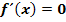 und zugleich
und zugleich 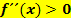
![]()

Bei einem HOPmuss der Graph eine waagrechte Tangente besitzen und rechtsgekrümmtsein und daher gilt: 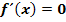 und zugleich
und zugleich 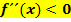
![]()

Erhältst du beim Einsetzen in 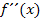 genau den Wert Null, handelt es sich vermutlich um einen Terrassenpunkt (TEP).
genau den Wert Null, handelt es sich vermutlich um einen Terrassenpunkt (TEP).
Bei einem TEP hat der Graph eine waagrechte Tangente und es ändert sich die Krümmung des Graphen von links nach rechts oder umgekehrt. In einem Terrassenpunkt ist der Graph also weder links- noch rechtsgekrümmt, er ist in diesem Punkt gar nicht gekrümmtund daher gilt: 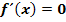 und zugleich
und zugleich 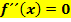
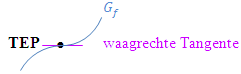
Dass es sich wirklich um einen TEP handelt, muss aber erst noch nachgewiesen werden. Ein Terrassenpunkt ist bekanntlich ein Wendepunkt mit waagrechter Tangente. Man muss also zeigen, dass wirklich ein Wendepunkt an dieser Stelle vorliegt. Bei einem Wendepunkt, und somit auch bei einem Terrassenpunkt, muss nicht nur 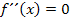 gelten;es muss sich auch das Vorzeichen der zweiten Ableitung ändern. Dies kann entweder mit Hilfe des Krümmungsverhaltens, z.B. mit einer Krümmungstabelle, nachgewiesen werden oder mit der dritten Ableitung, falls ihr
gelten;es muss sich auch das Vorzeichen der zweiten Ableitung ändern. Dies kann entweder mit Hilfe des Krümmungsverhaltens, z.B. mit einer Krümmungstabelle, nachgewiesen werden oder mit der dritten Ableitung, falls ihr 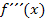 im Unterricht besprochen habt. (Die dritte Ableitung beschreibt die relative Veränderung der Krümmung. Das musst du nicht unbedingt wissen. Nur wenn ihr
im Unterricht besprochen habt. (Die dritte Ableitung beschreibt die relative Veränderung der Krümmung. Das musst du nicht unbedingt wissen. Nur wenn ihr 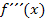 in der Schule tatsächlich besprochen habt, kannst du die dritte Ableitung benutzen, um einen Wendepunkt bzw. Terrassenpunkt nachzuweisen. Die dritte Ableitung darf an dieser Stelle nicht gleich Null sein. Man bildet also
in der Schule tatsächlich besprochen habt, kannst du die dritte Ableitung benutzen, um einen Wendepunkt bzw. Terrassenpunkt nachzuweisen. Die dritte Ableitung darf an dieser Stelle nicht gleich Null sein. Man bildet also 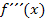 und setzt die entsprechende x-Koordinate
und setzt die entsprechende x-Koordinate 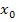 des vermutlichen Terrassenpunkts in
des vermutlichen Terrassenpunkts in 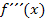 ein. Damit bei
ein. Damit bei 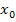 sicher ein TEP vorliegt, muss neben
sicher ein TEP vorliegt, muss neben 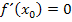 und
und 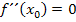 auch
auch 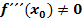 gelten.)
gelten.)
|
Zusammenfassung: Art der Extrema mit f´´(x) untersuchen
*Wenn ein Vorzeichenwechsel von Mit |
In diesem Zusammenhang sprechen manche Lehrer oft von einer sogenannten „notwendigen“ und von einer „hinreichenden“ Bedingung für die Existenz eines Extremums. Wahrscheinlich denkst du dir dabei:Was ist denn damit bloßwieder gemeint? Die Begriffe „notwendige“ und „hinreichende“ Bedingung tauchen in der Mathematik öfter auf, nicht nur bei der Definition eines Extremums, sondern beispielsweise auch bei Wendepunkten oder Terrassenpunkten. Im Folgenden werden die beiden Begriffe „notwendige“ und „hinreichende“ Bedingung speziell für die Existenz eines Extremums erklärt.
Damit an der Stelle 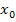 sicher ein relatives Extremum (HOP oder TIP) vorliegt und nicht etwa ein Terrassenpunkt, muss neben
sicher ein relatives Extremum (HOP oder TIP) vorliegt und nicht etwa ein Terrassenpunkt, muss neben 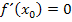 auch entweder
auch entweder 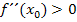 (TIP) oder
(TIP) oder 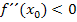 (HOP) gelten. Man kann also sagen, dass bei einem Extremum
(HOP) gelten. Man kann also sagen, dass bei einem Extremum 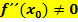 gelten muss. Dies ist zusammen mit der Bedingung
gelten muss. Dies ist zusammen mit der Bedingung 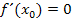 eine sogenannte „hinreichende“ Bedingung für einen Extrempunkt. Damit meint ein Mathematiker, dass die Bedingungen
eine sogenannte „hinreichende“ Bedingung für einen Extrempunkt. Damit meint ein Mathematiker, dass die Bedingungen 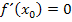 und zugleich
und zugleich 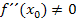 ausreichend (hinreichend) sind, damit ganz sicher bei
ausreichend (hinreichend) sind, damit ganz sicher bei 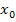 ein Extremum vorliegt. Wenn die Bedingung
ein Extremum vorliegt. Wenn die Bedingung 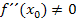 alleine gilt, muss jedoch nicht zwangsläufig ein Extremum vorliegen.
alleine gilt, muss jedoch nicht zwangsläufig ein Extremum vorliegen. 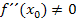 bedeutet alleine nur, dass der Funktionsgraph an der Stelle
bedeutet alleine nur, dass der Funktionsgraph an der Stelle 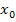 nicht die Krümmung 0 hat, d.h. er muss entweder links- oder rechtsgekrümmt sein. Nur weil der Graph nach links oder nach rechts gekrümmt ist, muss hier aber noch lange kein Extremum sein. Umgekehrt muss aber der Graph nach rechts gekrümmt sein, wenn ein HOP vorliegt, bzw. er muss nach links gekrümmt sein, wenn ein TIP vorliegt.
nicht die Krümmung 0 hat, d.h. er muss entweder links- oder rechtsgekrümmt sein. Nur weil der Graph nach links oder nach rechts gekrümmt ist, muss hier aber noch lange kein Extremum sein. Umgekehrt muss aber der Graph nach rechts gekrümmt sein, wenn ein HOP vorliegt, bzw. er muss nach links gekrümmt sein, wenn ein TIP vorliegt.
Nur zusammen mit der für ein Extremum „notwendigen“ Bedingung 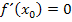 (waagrechte Tangente) lässt die Bedingung
(waagrechte Tangente) lässt die Bedingung 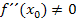 eindeutig den Schluss zu, dass die Funktion
eindeutig den Schluss zu, dass die Funktion  an der Stelle
an der Stelle 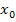 sicher einen Extrempunkt aufweist.
sicher einen Extrempunkt aufweist.
Für ein Extremum notwendige Bedingung: ![]()
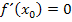
Das heißt, dass diese Bedingung erfüllt sein muss, damit überhaupt ein Extremum vorliegen kann. Ein Punkt muss eine waagrechte Tangente, also die Steigung 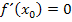 haben, damit es sich um ein Extremum handeln kann. Da aber auch Terrassenpunkte eine waagrechte Tangente besitzen, erfüllen auch sie die Bedingung
haben, damit es sich um ein Extremum handeln kann. Da aber auch Terrassenpunkte eine waagrechte Tangente besitzen, erfüllen auch sie die Bedingung 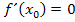 . Es kann sich daher an der Stelle
. Es kann sich daher an der Stelle 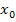 entweder um ein Extremum oder einen Terrassenpunkt handeln. Von der Bedingung
entweder um ein Extremum oder einen Terrassenpunkt handeln. Von der Bedingung 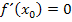 kann also noch nicht sicher auf die Existenz eines Extremums an der Stelle
kann also noch nicht sicher auf die Existenz eines Extremums an der Stelle 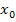 geschlossen werden. (Dazu braucht man noch eine hinreichende Bedingung.) Damit aber überhaupt ein Extremum vorliegen kann, ist es notwendig, dass
geschlossen werden. (Dazu braucht man noch eine hinreichende Bedingung.) Damit aber überhaupt ein Extremum vorliegen kann, ist es notwendig, dass 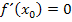 erfüllt ist. Daher die Bezeichnung „notwendige“ Bedingung.
erfüllt ist. Daher die Bezeichnung „notwendige“ Bedingung.
Für ein Extremum hinreichende Bedingung: 1. Möglichkeit:Vorzeichenwechsel von 
![]() 2. Möglichkeit:
2. Möglichkeit: 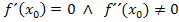
Das heißt, dass eine dieser Bedingungen ausreicht (hinreichend ist), damit man ganz sicher sagen kann, dass an der Stelle 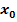 ein Extremum sein muss.
ein Extremum sein muss.
Warum man vom Vorzeichen von 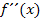 auf die Art der Extrema schließen kann, wird noch ausführlicher besprochen im Kapitel Zweite Ableitung f´´(x)Der Nachweis eines Terrassenpunktes mit
auf die Art der Extrema schließen kann, wird noch ausführlicher besprochen im Kapitel Zweite Ableitung f´´(x)Der Nachweis eines Terrassenpunktes mit 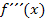 wird im Kapitel Wendepunkte mit dritter Ableitung nachweisen erläutert.
wird im Kapitel Wendepunkte mit dritter Ableitung nachweisen erläutert.
Jetzt aber wieder konkret zu unserem Beispiel. Es sollen Art und Lage der Extrema von  berechnet werden.
berechnet werden.
Hier noch einmal die Funktionsgleichung: 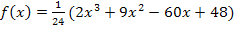
![]()
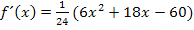
Wir haben bereits berechnet:
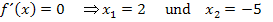
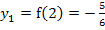
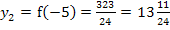
Jetzt bilden wir die zweite Ableitung 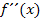 , indem wir
, indem wir  noch einmal mit Hilfe der Ableitungsregeln differenzieren (ableiten).
noch einmal mit Hilfe der Ableitungsregeln differenzieren (ableiten).
Erste Ableitung (von oben): 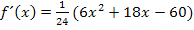
Zweite Ableitung:![]()
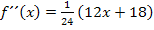
Wenn dir nicht klar ist, wie man von  auf
auf 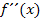 kommt, wiederhole noch einmal das Kapitel Einfache Ableitungsregeln. Um
kommt, wiederhole noch einmal das Kapitel Einfache Ableitungsregeln. Um 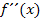 zu bilden, leitet man die erste Ableitung
zu bilden, leitet man die erste Ableitung  einfach noch einmal ab. Die Ableitungsregeln wurden also noch einmal auf die erste Ableitung
einfach noch einmal ab. Die Ableitungsregeln wurden also noch einmal auf die erste Ableitung  angewendet. Dadurch erhält man
angewendet. Dadurch erhält man 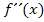 .
.
Jetzt klammern wir bei 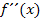 noch den Faktor 6 aus. Das muss zwar nicht sein, doch sieht das Ergebnis dann etwas schöner aus. (Bei
noch den Faktor 6 aus. Das muss zwar nicht sein, doch sieht das Ergebnis dann etwas schöner aus. (Bei  hätte man dies übrigens auch schon machen können.) Dadurch erhalten wir:
hätte man dies übrigens auch schon machen können.) Dadurch erhalten wir:
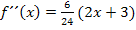
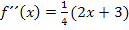
Nun müssen wir die x-Koordinaten der Punkte mit waagrechten Tangenten, hier 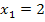 und
und 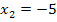 , in die zweite Ableitung einsetzen.
, in die zweite Ableitung einsetzen.
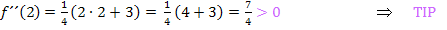
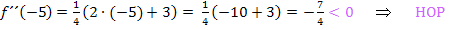
Im Prinzip sind wir jetzt schon fertig. Bei x = 2 liegt also ein relativer Tiefpunkt vor und bei x = -5 ein relativer Hochpunkt. Die entsprechenden y-Koordinaten haben wir oben schon berechnet. (Vorsicht:Nicht die Ergebnisse der zweiten Ableitung jeweils als y-Koordinate verwenden! 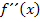 stellt ja die Krümmung an dieser Stelle und nicht y dar! Die Funktionswerte
stellt ja die Krümmung an dieser Stelle und nicht y dar! Die Funktionswerte 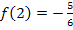 und
und 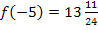 sind hier die y-Koordinaten. Vergleiche oben!) Wir schreiben die Koordinaten der Extrema noch schön auf. Sie lauten:
sind hier die y-Koordinaten. Vergleiche oben!) Wir schreiben die Koordinaten der Extrema noch schön auf. Sie lauten:
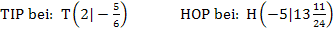
Mit der zweiten Ableitung geht die Unterscheidung zwischen HOP, TIP und TEP wirklich recht leicht. Nun wirst du dir vielleicht denken, dass du die andere Methode mit der Monotonie gar nicht mehr brauchst. Leider muss ich dich da enttäuschen! Du solltest trotzdem auch das Monotonieverhalten einer Funktion überprüfen und daraus auf eventuell vorhandene Extrema schließen können. Warum? Erstens gibt es Aufgaben, wo die Monotonie speziell überprüft werden soll, und zweitens wirst du es bald mit Funktionen zu tun bekommen, die sich nicht so schnell ein zweites Mal ableiten lassen. Wer hat denn schon Lust über eine halbe Seite nur an der zweiten Ableitung herumzurechnen, wenn man 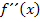 sonst gar nicht braucht, weil beispielsweise weder Wendepunkte noch das Krümmungsverhalten von
sonst gar nicht braucht, weil beispielsweise weder Wendepunkte noch das Krümmungsverhalten von  gefragt ist. Da verwendet man doch lieber das Monotonieverhalten, um die Art der Extrema zu untersuchen. Falls du beim Erstellen von Monotonietabellen noch Probleme hast – und das haben zu Beginn viele Schüler – solltest du noch einmal zurückgehen zum 8. Bsp., dort wird es im Folgenden ganz ausführlich besprochen, wie man eine Monotonietabelle erstellt. Lies dir das also auch die Methode mit der Monotonie genauestens durch, auch wenn die Aufgabe jetzt mit Hilfe von
gefragt ist. Da verwendet man doch lieber das Monotonieverhalten, um die Art der Extrema zu untersuchen. Falls du beim Erstellen von Monotonietabellen noch Probleme hast – und das haben zu Beginn viele Schüler – solltest du noch einmal zurückgehen zum 8. Bsp., dort wird es im Folgenden ganz ausführlich besprochen, wie man eine Monotonietabelle erstellt. Lies dir das also auch die Methode mit der Monotonie genauestens durch, auch wenn die Aufgabe jetzt mit Hilfe von 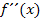 bereits gelöst ist!
bereits gelöst ist!
Ausführliche Lösung zu Bsp. 4b.)
Hier noch einmal alle gegebenen Graphen:
|
Abb. 7 |
Abb. 8 |
Abb. 9 |
|
Abb. 10 |
Abb. 11 |
Abb. 12 |
Welcher Graph stellt die Ableitungsfunktion von welchem dar? Wir sollen möglichst viele zusammengehörige Paare von Funktion und Ableitungsfunktion finden.
Lösung:
Abb. 7 stellt die Ableitung von Abb. 9 dar.
Abb. 10 stellt die Ableitung von Abb. 12 dar.
Abb. 11 stellt die Ableitung von Abb. 8 dar.
Erklärungen zur Lösung:
Wie kommt man darauf, dass nur Abb. 7 die Ableitung von Abb. 9 zeigen kann?
Betrachte noch einmal Abb. 9!
Der in Abb. 9 gezeigte Graph ist für 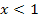 eine fallende Gerade mit der Steigung -1 und für
eine fallende Gerade mit der Steigung -1 und für 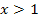 eine steigende Gerade mit der Steigung +1. (Es handelt sich bei Abb. 9 übrigens um den Graph der Funktion
eine steigende Gerade mit der Steigung +1. (Es handelt sich bei Abb. 9 übrigens um den Graph der Funktion 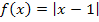 , die um 1 nach rechts verschobene Betragsfunktion.) Die Ableitung entspricht bekanntlich der Steigung der Funktion. Somit muss die Ableitung der in Abb. 9 gezeigten Funktion für
, die um 1 nach rechts verschobene Betragsfunktion.) Die Ableitung entspricht bekanntlich der Steigung der Funktion. Somit muss die Ableitung der in Abb. 9 gezeigten Funktion für 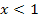 konstant -1 und für
konstant -1 und für 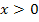 konstant +1 sein. Die Ableitungsfunktion muss zwangsläufig für
konstant +1 sein. Die Ableitungsfunktion muss zwangsläufig für 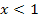 die waagrechte Gerade
die waagrechte Gerade 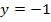 und für
und für 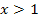 die waagrechte Gerade
die waagrechte Gerade 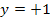 sein.
sein.
An der Stelle 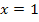 ist der in Abb. 9 gezeigte Graph nicht differenzierbar, d.h. man kann die Steigung der Tangente dort nicht eindeutig ermitteln. Der Graph der in Abb. 9 gezeigten Funktion hat hier eine Spitze. Man weißalso nicht, ob an der Stelle
ist der in Abb. 9 gezeigte Graph nicht differenzierbar, d.h. man kann die Steigung der Tangente dort nicht eindeutig ermitteln. Der Graph der in Abb. 9 gezeigten Funktion hat hier eine Spitze. Man weißalso nicht, ob an der Stelle 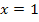 für die Steigung -1, +1 oder irgendein anderer Wert gilt. Die Ableitung ist an der Stelle
für die Steigung -1, +1 oder irgendein anderer Wert gilt. Die Ableitung ist an der Stelle 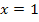 deshalb nicht definiert, was zu einer Definitionslücke der Ableitungsfunktion bei
deshalb nicht definiert, was zu einer Definitionslücke der Ableitungsfunktion bei 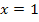 führt. Nun betrachte noch einmal die Abbildungen 7 bis 12!
führt. Nun betrachte noch einmal die Abbildungen 7 bis 12!
Was stellst du dabei fest?
Nur Abb. 7 erfüllt alle soeben beschriebenen Bedingungen.
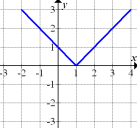
Abb. 9 |
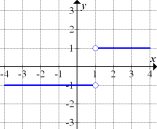
Abb. 7 |
Vorsicht:Abb. 10 kann nicht die Ableitung von Abb. 9 sein, da der in Abb. 10 gezeigte Graph für 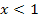 die waagrechte Gerade
die waagrechte Gerade 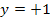 und für
und für 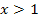 die waagrechte Gerade
die waagrechte Gerade 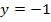 zeigt. D.h. die Vorzeichen wären falsch.
zeigt. D.h. die Vorzeichen wären falsch.
Vergleiche dazu noch einmal Abb.10!
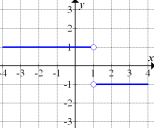
Abb. 10
Abb. 10 ist die Ableitung einer Funktion, die für 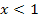 konstant mit der Steigung +1 steigt und für
konstant mit der Steigung +1 steigt und für 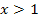 konstant mit der Steigung -1 fällt. Diese Bedingung erfüllt der Graph in Abb. 12. Daher stellt Abb. 10 die Ableitung von Abb. 12 dar. (In Abb. 12 ist übrigens der Graph der Funktion
konstant mit der Steigung -1 fällt. Diese Bedingung erfüllt der Graph in Abb. 12. Daher stellt Abb. 10 die Ableitung von Abb. 12 dar. (In Abb. 12 ist übrigens der Graph der Funktion 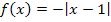 dargestellt;das ist die um 1 nach rechts verschobene und an der x-Achse gespiegelte Betragsfunktion.)
dargestellt;das ist die um 1 nach rechts verschobene und an der x-Achse gespiegelte Betragsfunktion.)
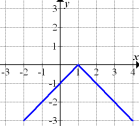
Abb. 12 |

Abb. 10 |
Wie kommt man darauf, dass Abb. 11 die Ableitung von Abb. 8 darstellt?
Betrachte dazu erst noch einmal Abb. 8!
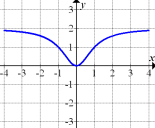
Abb. 8
Der in Abb. 8 dargestellte Graph hat bei 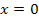 eine waagrechte Tangente. Daher muss die zugehörige Ableitungsfunktion bei
eine waagrechte Tangente. Daher muss die zugehörige Ableitungsfunktion bei 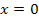 eine Nullstelle besitzen. Für
eine Nullstelle besitzen. Für 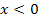 fällt der Graph, so dass die zugehörige Ableitungsfunktion unterhalb der x-Achse liegen muss. Für
fällt der Graph, so dass die zugehörige Ableitungsfunktion unterhalb der x-Achse liegen muss. Für 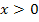 steigt der Graph, so dass die zugehörige Ableitungsfunktion oberhalb der x-Achse liegen muss. Für betragsmäßig große x (ganz weit links bzw. rechts im Koordinatensystem) verläuft der in Abb. 8 gezeigte Graph immer flacher;die Steigung nähert sich an Null an. Daher muss sich die zugehörige Ableitungsfunktion für x gegen
steigt der Graph, so dass die zugehörige Ableitungsfunktion oberhalb der x-Achse liegen muss. Für betragsmäßig große x (ganz weit links bzw. rechts im Koordinatensystem) verläuft der in Abb. 8 gezeigte Graph immer flacher;die Steigung nähert sich an Null an. Daher muss sich die zugehörige Ableitungsfunktion für x gegen 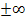 an Null annähern. Die Ableitungsfunktion zu der in Abb. 8 dargestellten Funktion hat deshalb zwangsläufig die x-Achse
an Null annähern. Die Ableitungsfunktion zu der in Abb. 8 dargestellten Funktion hat deshalb zwangsläufig die x-Achse 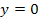 als waagrechte Asymptote. Diese Bedingungen erfüllt nur der in Abb. 11 gezeigte Graph. Deshalb kann nur Abb. 11 die Ableitungsfunktion zu der in Abb. 8 dargestellten Funktion zeigen.
als waagrechte Asymptote. Diese Bedingungen erfüllt nur der in Abb. 11 gezeigte Graph. Deshalb kann nur Abb. 11 die Ableitungsfunktion zu der in Abb. 8 dargestellten Funktion zeigen.

Abb. 8 |
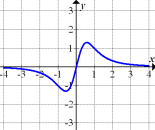
Abb. 11 |
Andere Paare aus Funktion und Ableitungsfunktion gibt es nicht.

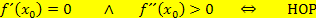
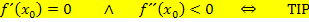
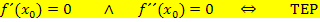 *
*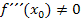 gilt.
gilt.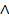 bedeutet „und zugleich“.
bedeutet „und zugleich“.