b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Da wir zur Berechnung von t später auch die y-Koordinate von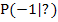 
brauchen, berechnen wir als erstes gleich ´mal 
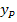. Da der Punkt P auf der Funktion 
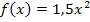liegt, erhalten wir seine y-Koordinate 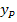durch Einsetzen der x-Koordinate von P in die Funktionsgleichung;d.h. wir müssen hier 
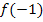bilden.
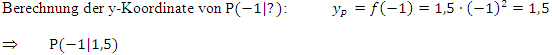
Nun müssen wir uns an die Berechnung der Tangentensteigung im Punkt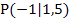 
machen. Da die Ableitung 
bekanntlich der Tangentensteigung an der Stelle x entspricht, müssen wir als nächstes bilden und dann die x-Koordinate von P in die Ableitung einsetzen. In anderen Worten:Man erhält die Tangentensteigung m im Punkt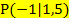 
, indem man die x-Koordinate x = -1 für x in die Ableitung einsetzt.
Hier noch einmal die Funktionsgleichung: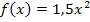
1. Ableitung bilden: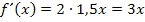 
(Vergleiche:Einfache Ableitungsregeln)
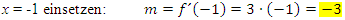
Die Tangentensteigung im Punkt P wissen wir jetzt;es gilt:m = -3
Um die Gleichung der Tangente in P aufstellen zu können, fehlt uns nur noch der y-Achsenabschnitt t. Wir können t leicht berechnen, indem wir in y = mx + t für m den soeben berechneten Wert -3 sowie für x bzw. y die Koordinaten von 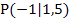einsetzen und dann nach t auflösen.
y = mx + t
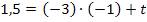
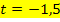
Nun setzten wir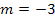 
und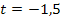 
in die allgemeine Geradengleichung y = mx + t ein. Achtung:Für x und y darf jetzt nichts mehr eingesetzt werden! Also jetzt nicht mehr die Koordinaten von P für x und y einsetzen! Es soll schließlich eine Geradengleichung (die Tangentengleichung) aufgestellt werden und dabei müssen x und y als Variablen (d.h. als Buchstaben) vorkommen. So erhalten wir die gesuchte Tangentengleichung.
Tangente: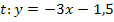 
Anmerkung:Der Buchstabe t vor dem Doppelpunkt ist nur die Bezeichnung der Tangente, welche t genannt wird. Dieses t hat also nichts mit dem y-Achsenabschnitt, der dummerweise ebenfalls t heißt, zu tun. Es ist leider etwas verwirrend, dass t einmal die Bezeichnung der Tangente ist, und einmal für den y-Achsenabschnitt steht.
Zusätzlich zur Tangentengleichung ist in dieser Teilaufgabe nach dem Schnittwinkel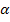 
der Tangente mit der x-Achse gefragt. Dafür brauchen wir die folgende Formel:
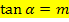
Wir setzen für m den vorher berechneten Wert der Tangentensteigung -3 ein.
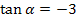
Mit dem Taschenrechner (Mode:DEG) und der Tastenkombination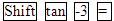 
erhältst du den gesuchten Winkel.
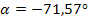
Hinweis für G8-Schüler:Merke dir die Formel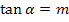 
für den Schnittwinkel mit der x-Achse auswendig. Sie steht nicht auf der Merkhilfe, obwohl man sie immer ´mal wieder in Prüfungen braucht.
Hinweis für FOS/BOS-Schüler:Es ist zwar gut, wenn du die Formel 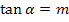auswendig weißt. Du findest sie aber auch in der orangen bsv-Formelsammlung.
