Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
Wir lösen die Nebenbedingung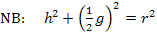 
nach g auf. (Denk daran, dass r eine Konstante, also eine feste Zahl ist und keine Variable! Auflösen nach r würde daher nichts bringen. Man muss schließlich nach einer der Variablen auflösen, d.h. entweder nach g oder nach h, aber eben nicht nach r. Wir könnten auch nach h auflösen. Doch müsste man dann mit Brüchen rechnen. Daher ist es besser nach g aufzulösen;dabei entstehen nämlich keine Brüche.)
Auflösen der Nebenbedingung nach g:
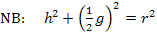
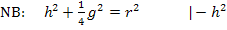
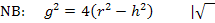
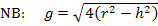
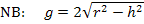
Vorsicht:Dieser Ausdruck lässt sich nicht weiter vereinfachen! Die Wurzel darf keinesfalls einzeln aus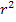 
und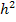 
gezogen werden.
Beachte also: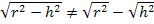 
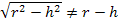
Merke:Aus Differenzen oder Summen darf die Wurzel nicht einzeln gezogen werden. Einfacher gesagt:Steht ein Plus oder Minus unter der Wurzel, darfst du die Wurzel nicht aus den einzelnen Faktoren ziehen.
Wäre unter der Wurzel dagegen ein Produkt gestanden, dann hätte man die Wurzel einzeln ziehen dürfen: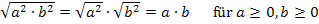 
Merke:Aus Produkten darf die Wurzel einzeln gezogen werden. Einfacher gesagt:Steht ein Mal-Punkt unter der Wurzel, darfst die Wurzel aus den einzelnen Faktoren ziehen. Das gleiche gilt für Quotienten, da darfst du auch aus Zähler und Nenner einzeln die Wurzel ziehen.
Jetzt setzen wir die nach g aufgelöste Nebenbedingung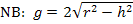 
in die Hauptbedingung 
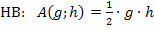ein, um die Zielfunktion zu erhalten. Dadurch fällt die Variable g heraus;die Zielfunktion enthält somit nur noch die Variable h.
NB in HB: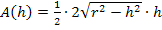 
Nach Kürzen mit 2 ergibt sich:
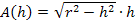
Wir ziehen h noch unter die Wurzel:
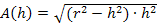
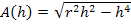
Dies ist nun die Zielfunktion. Leider ist sie wegen der Wurzel ziemlich kompliziert;man bräuchte zum Ableiten die Kettenregel. (Näheres dazu bei:Die Kettenregel) Wenn man jedoch wieder den Trick anwendet, der schon im 2. Bsp. gezeigt wurde, geht es viel einfacher. Wir nehmen statt der eigentlichen Zielfunktion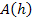 
ihr Quadrat 
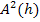. Dadurch fällt die Wurzel weg und wir können auf die Kettenregel beim Ableiten verzichten. Das Ergebnis einer Wurzel ist schließlich maximal, wenn der Ausdruck unter der Wurzel maximal ist. Damit wir nicht andauernd 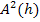für die Ersatzzielfunktion schreiben müssen, führen wir dafür eine neue Bezeichnung ein. Wir legen fest:
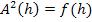
Unsere Ersatzzielfunktion, also das Quadrat der eigentlichen Zielfunktion, lautet somit:
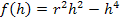
4. Schritt:Definitionsmenge der Ersatzzielfunktion angeben
Da es sich sowohl bei g als auch bei h um Streckenlängen handelt, muss auf jeden Fall gelten:
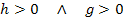
Die Grundlinie g haben wir bereits in Abhängigkeit von h angegeben:
