Herleitung der Tangentensteigung aus der Sekantensteigung mittels des Differenzialquotienten

Könnte man jedoch die Steigung der Tangente im Punkt P an die Funktion 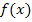berechnen, wäre unser Problem gelöst. Durch den Punkt P und die zugehörige Tangentensteigung ist die Tangente nämlich eindeutig festgelegt. Man bräuchte nur noch vom Punkt P ausgehend ein Steigungsdreieck zeichnen und erhielte so einen zweiten Punkt der Tangente, so dass sie sich leicht zeichnen ließe. Wir müssen also die Tangentensteigung im Punkt P berechnen. Aber wie geht das?

Eigentlich braucht man zwei verschiedene Punkte, um die Steigung einer Geraden zu berechnen. Von der Tangente kennen wir aber nur einen einzigen Punkt, nämlich den Berührpunkt P mit dem Graphen .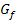

Die Antwort auf die Frage, wie man die Tangentensteigung berechnen kann, liefert die Differenzialrechnung. Mit Hilfe der Differenzialrechnung kann die Steigung der Tangente in jedem beliebigen Punkt P des Graphen ermittelt werden.

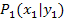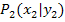Vorweg wiederholen wir noch kurz, wie man mit zwei gegebenen Punkten und die Steigung m einer Geraden durch 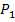und 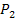berechnet. Ohne die folgende Formel für die Berechnung der Steigung m einer Geraden 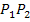kommen wir nämlich nicht zur Steigung der Tangente. Die komplette Herleitung der Tangentensteigung basiert auf der folgenden Formel für die Steigung mit zwei Geradenpunkten!

Wiederholung:

Gegeben sind die beiden Geradenpunkte 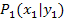und 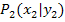. Gesucht ist die Steigung m der Geraden 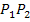. In der folgenden Abbildung kannst du in Rosa das Steigungsdreieck sehen. Um die Steigung m der Geraden 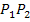zu ermitteln, muss man sich die Länge der rosafarbenen senkrechten Strecke und die Länge der rosafarbenen waagrechten Strecke überlegen. Beginnen wir mit der waagrechten Strecke des Steigungsdreiecks. Die Punkte 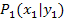und 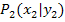sind, wie gesagt, als gegeben zu betrachten.

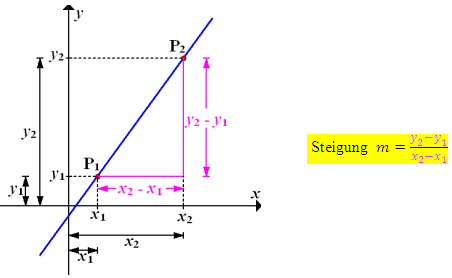
Abb.:Zur Berechnung der Steigung einer Geraden durch die Punkte 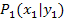und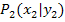

Stelle dir zur Vereinfachung konkrete Zahlen für die Koordinaten der beiden Punkte vor. Zum Beispiel: 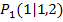und 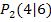Das sind absolut beliebig gewählte Zahlen, abgesehen davon, dass die x-Koordinaten der beiden Punkte verschieden sein müssen. Damit es dir leichter fällt, dies mit der gezeigten Abbildung in Zusammenhang zu bringen, wurde bei dem konkreten Zahlenbeispiel 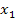kleiner als 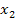gewählt und 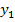kleiner als .

---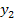