Die h-Methode

Wir wollen die Steigung einer gegebenen Funktion 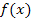in einem bestimmten Punkt 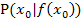berechnen, also die Steigung der Tangente an 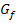in diesem Punkt.

Wir bleiben bei unserem Einführungsbeispiel 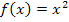mit dem Punkt 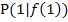. Wie kann man nun die Tangentensteigung im Punkt P berechnen?

Wir wählen zuerst einen Hilfspunkt H, der ebenfalls auf dem Graphen und in der Nähe von P liegt. Den Unterschied der x-Koordinaten von P und H nennen wir ab sofort h. Es sei:h >0 Da der Punkt P die x-Koordinate 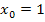besitzt, hat H dann die x-Koordinate 1 + h. Betrachte dazu die unten folgende Abbildung!

Mit Hilfe der Abbildung kannst du dir den Sachverhalt hoffentlich einigermaßen vorstellen. In Rosa ist schon einmal das Steigungsdreieck der Sekante eingezeichnet.

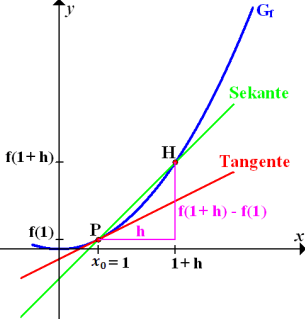
Abb.:Zur Berechnung der Tangentensteigung von 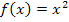im Kurvenpunkt 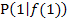mit der h-Methode. (Die Normalparabel sieht in der Abbildung nur deshalb breiter aus, als du es gewohnt bist, weil hier ein anderer Maßstab auf den Achsen gewählt wurde als sonst üblich.)

Da H ein Punkt des Graphen sein soll, kann man für die y-Koordinate von H  allgemein 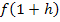schreiben. Die y-Koordinate eines Kurvenpunktes der Funktion 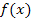wird ja bekanntlich berechnet, indem man die x-Koordinate in die Funktionsgleichung 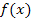einsetzt. So hätte beispielsweise ein Punkt mit der x-Koordinate 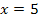die y-Koordinate 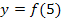. Dem entsprechend hat der Punkt H mit der x-Koordinate 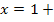h eben die y-Koordinate .

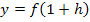Durch den gegebenen Punkt P und den Hilfspunkt H zeichnen wir eine Gerade. Die Gerade PH ist dann eine Sekante zu 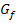, weil sie den Graphen zweimal schneidet, nämlich in P und in H. Dann ermitteln wir erst einmal die Steigung der Sekante PH. (Später schieben wir dann den Hilfspunkt H in Gedanken beliebig nah an den Punkt P heran, d.h. wir lassen h gegen Null gehen. Dadurch wird aus der Sekante die Tangente und aus der Sekantensteigung letztendlich die gesuchte Tangentensteigung.)

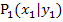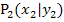Die Steigung der Sekante lässt sich mit der folgenden bekannten Formel für die Steigung einer Geraden durch die zwei Punkte und berechnen:

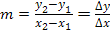
Unsere Punkte heißen natürlich nicht 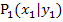und 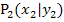, sondern 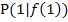und Hilfspunkt 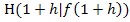. Setzen wir die Koordinaten unserer Punkte in die Formel für die Steigung einer Geraden ein, erhalten wir den Differenzenquotienten an der Stelle 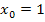. Das entspricht der Sekantensteigung .

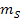Sekantensteigung 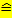Differenzenquotient: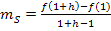

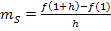
Um von der Sekante PH zur Tangente im Punkt P zu kommen, müssen wir den Hilfspunkt H immer näher an P heran schieben. Der Unterschied der x-Koordinaten h muss also beliebig klein werden. Man sagt h geht gegen Null. So wird aus dem Differenzenquotient, der bloßder Sekantensteigung entspricht, der sogenannte Differenzialquotient, welcher dann der gesuchten Tangentensteigung entspricht.

Tangentensteigung im Punkt 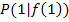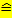Differenzialquotient: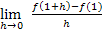

Anmerkung:Die Schreibweise 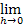(sprich:„Limes h gegen Null“) drückt aus, dass h beliebig klein, also fast gleich Null wird.

---