Stetigkeit und Differenzierbarkeit
Bei der Gerade steht dagegen nur das „Größer-Zeichen“, nicht aber das „Größer-Gleich-Zeichen“. An der Stelle  gilt also die Parabel und nicht die Gerade.)
gilt also die Parabel und nicht die Gerade.)
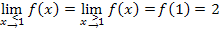
Deshalb ist die Funktion  an der Stelle
an der Stelle  stetig;sie hat hier keine Sprungstelle. Die beiden Teilgraphen stoßen genau im Punkt
stetig;sie hat hier keine Sprungstelle. Die beiden Teilgraphen stoßen genau im Punkt 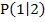 zusammen.
zusammen.
| Zusammenfassung:
Überprüfung der Stetigkeit an der Stelle Die Stelle · Berechnung der folgenden beiden Grenzwerte:
Anmerkung:
· Berechnung des Funktionswertes · Sind alle drei Ergebnisse gleich, ist die Funktion Sind zwar die beiden Grenzwerte gleich, die Funktion ist aber an der Stelle |
Weil die Überprüfung der Stetigkeit mit der h-Methode ziemlich kompliziert ist, schauen wir uns gleich noch einige weitere Beispiele an.
1. Bsp.:
Gegeben ist die Funktion 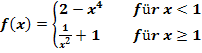
Ist die Funktion 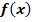 an der Stelle
an der Stelle 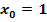 stetig?
stetig?
Lösung:
Hier soll untersucht werden, ob die Funktion  an der Stelle
an der Stelle  stetig ist. Warum überhaupt an der Stelle
stetig ist. Warum überhaupt an der Stelle  ? Ganz einfach, weil bei
? Ganz einfach, weil bei  die Nahtstelle der beiden Teilfunktionen ist. Die eine Teilfunktion
die Nahtstelle der beiden Teilfunktionen ist. Die eine Teilfunktion 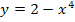 gilt schließlich für
gilt schließlich für 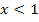 und die andere Teilfunktion
und die andere Teilfunktion 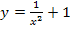 für
für 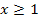 . Die Frage ist also, ob die beiden Teilgraphen bei
. Die Frage ist also, ob die beiden Teilgraphen bei 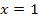 wirklich zusammentreffen, oder ob bei
wirklich zusammentreffen, oder ob bei 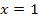 eine Sprungstelle vorliegt. Wir wollen beide Methoden zur Überprüfung der Stetigkeit anschauen.
eine Sprungstelle vorliegt. Wir wollen beide Methoden zur Überprüfung der Stetigkeit anschauen.
1. Methode:Einsetzten von 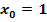 in die beiden Teilfunktionen
in die beiden Teilfunktionen
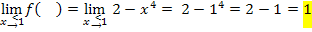
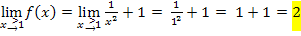
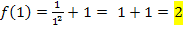
Es ergibt sich nicht dreimal dasselbe Ergebnis. Daher ist die Funktion  bei
bei  nicht stetig. Der Graph hat also eine Sprungstelle bei
nicht stetig. Der Graph hat also eine Sprungstelle bei  .
.
2. Methode:Überprüfung der Stetigkeit mit der „h-Methode“

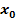 mit der h-Methode
mit der h-Methode ist dabei die Nahtstelle der Teilfunktionen, also eine konkrete Zahl. Im Folgenden steht h für eine kleine, positive Zahl. Es gilt also:
ist dabei die Nahtstelle der Teilfunktionen, also eine konkrete Zahl. Im Folgenden steht h für eine kleine, positive Zahl. Es gilt also: 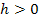
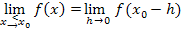
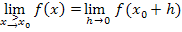
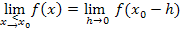 wird berechnet, indem man bei derjenigen Teilfunktion, die für
wird berechnet, indem man bei derjenigen Teilfunktion, die für 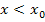 gilt,
gilt, 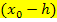
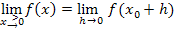 wird berechnet, indem man bei derjenigen Teilfunktion, die für
wird berechnet, indem man bei derjenigen Teilfunktion, die für 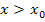 gilt,
gilt, 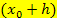
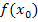 , d.h. bei derjenigen Teilfunktion, wo
, d.h. bei derjenigen Teilfunktion, wo 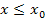 oder
oder 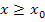 steht (also das Gleichheitszeichen dabei ist),
steht (also das Gleichheitszeichen dabei ist), 