Zweite Ableitung f´´(x)

als nächstes berechnen wir die zugehörigen y-Koordinaten, indem wir die soeben ermittelten x-Koordinaten in die Funktionsgleichung 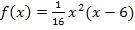einsetzen.

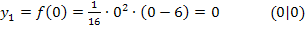
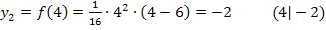
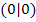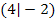Zu den Punkten mit waagrechten Tangenten gehören bekanntlich die Hochpunkte, Tiefpunkte, aber auch die Terrassenpunkte. Um herauszufinden, ob es sich bei den Punkten und jeweils um einen relativen Hochpunkt, einen relativen Tiefpunkt oder um einen Terrassenpunkt (kein Extremum) handelt, setzten wir danach die x-Koordinaten dieser Punkte in die zweite Ableitung ein.

Zur Erinnerung:

*

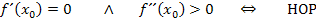
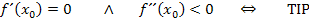
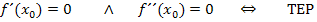*Wenn ein Vorzeichenwechsel von an der Stelle vorliegt bzw. 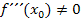gilt.

Wir bilden deshalb erst einmal die zweite Ableitung.

Hier noch einmal die erste Ableitung:

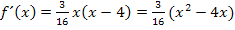
Damit man die zweite Ableitung ohne Produktregel bilden kann, wurde bei das x in die Klammer hineinmultipliziert.

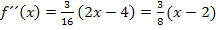
Beim letzten Schritt wurde die Zahl 2 ausgeklammert. Das muss nicht unbedingt gemacht werden, doch macht es die zweite Ableitung noch etwas „schöner“.

Nun setzten wir die x-Koordinaten der Punkte mit waagrechten Tangenten 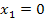und 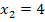in die zweite Ableitung ein, um die Art der Extrema herauszufinden.

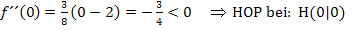
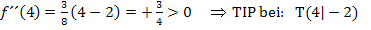
Damit ist die Aufgabe gelöst. Du konntest daran sehen, dass sich die Art der Extrema mit Hilfe der zweiten Ableitung wesentlich schneller herausfinden ließ, als wenn wir die Monotonie der Funktion untersucht hätten. Leider lässt sich die zweite Ableitung nicht bei allen Funktionen so einfach und schnell bilden wie in diesem Beispiel. Muss man beispielsweise die zweite Ableitung durch aufwendige Rechnung mit Produkt-, Quotienten- und/oder Kettenregel berechnen, kann es auch ratsam sein, die Art der Extrema doch mit Hilfe der Monotonieuntersuchung zu bestimmen.

7. Bsp.:

Gegeben ist die Funktion .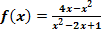

a.) Ermittle Art und Lage des relativen Extremums!

b.) Untersuche das Krümmungsverhalten der Funktion und gib die Koordinaten des Wendepunkts an.

Lösung:

Bevor wir anfangen die Funktion abzuleiten, formen wir sie noch etwas um. Im Nenner kann die zweite binomische Formel 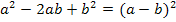angewendet werden.

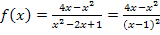
In dieser Form lässt sich die Ableitung besser ermitteln und die maximale Definitionsmenge der Funktion leicht ablesen. Für 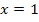würde der Nenner Null ergeben. Daher liegt bei 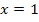eine Definitionslücke vor.

---