1. Flächenberechnungenmit Hilfe von Integralen
Wenn eine Funktion stetig ist, muss nur noch gezeigt werden, dass sie streng monoton ist. Dadurch wird bewiesen, dass die Funktion umkehrbar ist. Die Monotonie untersucht man mit der ersten Ableitung der Funktion. Das Vorzeichen von 
darf sich nicht ändern, damit die Funktion streng monoton ist.
Um zu beweisen, dass 
in ihrer gesamten Definitionsmenge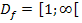 
umkehrbar ist, muss demnach nur noch gezeigt werden, dass die erste Ableitung für beliebige reelle Werte von x entweder immer positiv oder immer negativ ist.
Bei handelt es sich um eine verkettete Funktion. (Siehe auch:Verkettete Funktion/Verkettung) Wir leiten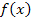 
daher mit Hilfe der Kettenregel ab. Wenn du die Ableitung der Wurzelfunktion auswendig weißt, kannst du folgendermaßen vorgehen:
Zur Erinnerung:
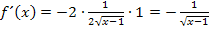
Hinweis:
Die Ableitung der Wurzelfunktion 
solltest du an sich auswendig wissen. Falls du sie jedoch (noch) nicht weißt, kannst du sie folgendermaßen herleiten:Die (zweite) Wurzel mit dem Potenzgesetz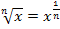 
als Potenz 
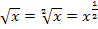schreiben, mit der Regel 
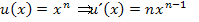ableiten und zum Schluss wieder ohne Potenz schreiben, also die Ableitung mit dem Potenzgesetz 
umformen.
(Näheres dazu bei Einfache Ableitungsregeln)
Dir ist nicht klar, warum oben beim Ableiten der Funktion 
zuerst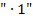 
dazu geschrieben wurde?
Bei der verketteten Funktion ist der Radikand x – 1 die innere Funktion. Die Ableitung davon ist 1. Nachdifferenzieren bedeutet, dass man beim Ableiten einer verketteten Funktion zum Schluss noch mit der Ableitung der inneren Funktion multiplizieren muss. Die Multiplikation mit der Zahl 1 entspricht hier also dem Nachdifferenzieren. Daher kommt der Faktor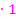 
bei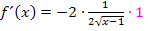 
. Man kann diese 1 natürlich letztendlich weglassen.
Nun müssen wir die Monotonie von untersuchen, also das Vorzeichen der Ableitung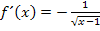 
.
Wie bei den Überlegungen zur Wertemenge schon besprochen, ist das Ergebnis einer Wurzel niemals negativ. Gleich 0 kann der Nenner sowieso nicht sein, da die Division durch 0 nicht definiert ist. (Die Ableitung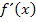 
ist nur für x >1 definiert, aber nicht für x = 1.) Der Nenner der Ableitung ist also immer positiv. Die Zahl 1 im Zähler der Ableitung ist ebenfalls positiv. Mit dem Minuszeichen davor ergibt sich immer etwas Negatives. Daher ist die Ableitung grundsätzlich negativ und der Graph 
streng monoton fallend.
Die Funktion ist stetig und streng monoton, deshalb für x 
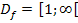umkehrbar.
Ermittlung der Umkehrfunktion:
Wir vertauschen bei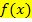 
jeweils x und y gegeneinander;d.h. für y schreibt man x und statt x schreibt man entsprechend y. Danach muss wieder nach y aufgelöst werden. (Alternativ dazu kann man bei auch zuerst nach x auflösen und erst am Schluss jeweils x und y gegeneinander vertauschen. Das liefert ebenfalls die Gleichung der Umkehrfunktion.)
