3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen
· Ermittlung der Umkehrfunktion 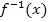 :
:
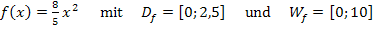
Anmerkung:Ist eine Funktion 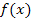 in der angegebenen Definitionsmenge
in der angegebenen Definitionsmenge 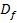 streng monoton (also nur steigend oder nur fallend), kommt man auf die Wertemenge
streng monoton (also nur steigend oder nur fallend), kommt man auf die Wertemenge 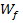 , indem man die Randpunkte der Definitionsmenge
, indem man die Randpunkte der Definitionsmenge 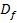 in die Funktionsgleichung
in die Funktionsgleichung 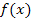 einsetzt.
einsetzt.
In diesem Beispiel ist die Definitionsmenge laut Angabe 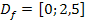 . Die Randpunkte liegen somit bei x = 0 und x = 2,5. Diese beiden Zahlen müssen wir daher in
. Die Randpunkte liegen somit bei x = 0 und x = 2,5. Diese beiden Zahlen müssen wir daher in 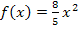 einsetzen:
einsetzen:
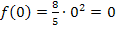
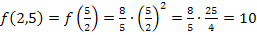
Somit ergibt sich die Wertemenge 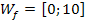 . Wir benötigen die Wertemenge
. Wir benötigen die Wertemenge 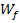 , da sich daraus die Definitionsmenge der Umkehrfunktion
, da sich daraus die Definitionsmenge der Umkehrfunktion 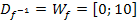 und somit die Integrationsgrenzen a = 0 und b = 10 ergeben.
und somit die Integrationsgrenzen a = 0 und b = 10 ergeben.
Jetzt bilden wir die Umkehrfunktion. Statt 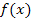 schreiben wir als erstes y:
schreiben wir als erstes y:
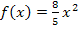
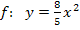
Nun vertauschen wir x und y gegeneinander;ab dann liegt schon 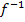 vor:
vor:
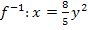
Dies ist bereits die Umkehrfunktion 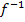 . Sie ist aber noch nicht nach y aufgelöst;wir brauchen
. Sie ist aber noch nicht nach y aufgelöst;wir brauchen 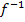 jedoch in der nach y aufgelösten Form. Deshalb stellen wir im nächsten Schritt nach y um:
jedoch in der nach y aufgelösten Form. Deshalb stellen wir im nächsten Schritt nach y um:
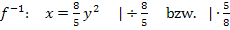
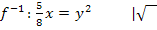
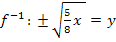
In unserem Fall gilt das Pluszeichen. Das erkennt man an der Wertemenge 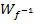 der Umkehrfunktion, die bekanntlich der Definitionsmenge
der Umkehrfunktion, die bekanntlich der Definitionsmenge 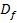 der Funktion selbst entspricht. Somit gilt hier:
der Funktion selbst entspricht. Somit gilt hier: 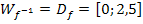
Bei der Umkehrfunktion dürfen also keine negativen Werte herauskommen, sondern nur Zahlen von 0 bis 2,5. Dies ist der Grund, warum das Minuszeichen vor der Wurzel wegfällt.
Die gesuchte Umkehrfunktion lautet daher:
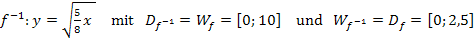
Oder anders geschrieben:
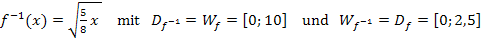
· Berechnung des Volumens mit der Formel:
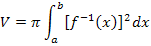
Die Integrationsgrenzen ergeben sich aus der Definitionsmenge der Umkehrfunktion 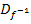 bzw. der Wertemenge
bzw. der Wertemenge 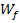 der Funktion
der Funktion 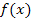 . Wegen
. Wegen 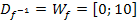 müssen wir von a = 0 bis b = 10 integrieren.
müssen wir von a = 0 bis b = 10 integrieren.
Mit a = 0 und b = 10 sowie 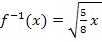 ergibt sich:
ergibt sich:
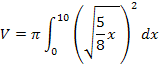
Damit du dir die Zusammenhänge besser vorstellen kannst, fertigen wir eine Skizze an, die den Graph der Funktion 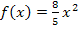 mit x
mit x  [0;2,5] und den Graph der zugehörigen Umkehrfunktion
[0;2,5] und den Graph der zugehörigen Umkehrfunktion 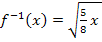 zeigt. Der Graph
zeigt. Der Graph  rotiert um die y-Achse;der Graph
rotiert um die y-Achse;der Graph 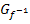 der Umkehrfunktion rotiert dagegen um die x-Achse. Betrachte dazu die folgende Abbildung!
der Umkehrfunktion rotiert dagegen um die x-Achse. Betrachte dazu die folgende Abbildung!
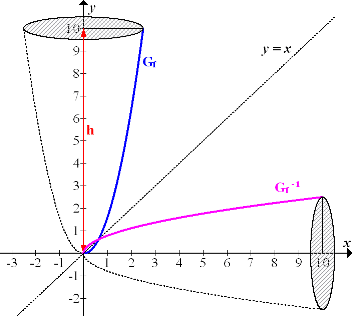
Abb.:Zur Berechnung des Volumens des Sektkelches mit Hilfe der Umkehrfunktion:Durch die Rotation des Graphen 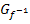 der Umkehrfunktion
der Umkehrfunktion 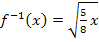 mit x
mit x  [0;10] um die x-Achse entsteht ein Rotationskörper, der das gleiche Volumen hat wie der Rotationskörper, der durch die Rotation des Graphen
[0;10] um die x-Achse entsteht ein Rotationskörper, der das gleiche Volumen hat wie der Rotationskörper, der durch die Rotation des Graphen  der Funktion
der Funktion 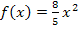 mit x
mit x  [0;2,5] um die y-Achse entsteht.
[0;2,5] um die y-Achse entsteht.
![]()
Nun müssen wir nur noch das Integral ausrechnen.
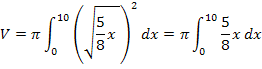
Integration nach dx liefert:

