Die Integralfunktion und der HDI

1. Bsp.:

Ermittle die integralfreie Darstellung der folgenden Integralfunktionen!

a.)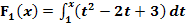

b.)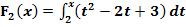

c.)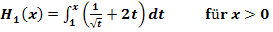

Lösung:

Um die integralfreie Darstellung der Integralfunktionen zu ermitteln, müssen wir die Integrale ausrechnen, also in einem ersten Schritt integrieren mit Hilfe der folgenden Regel:

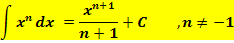
Das bedeutet, dass du zum Exponenten 1 dazu zählen und außerdem durch den neuen Exponenten teilen sollst, wenn du 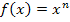integrierst, also wenn du eine Stammfunktion F(x) einer Funktion der Form 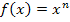suchst.

Wir integrieren allerdings nach t und nicht nach x. Daher steht bei uns jetzt statt x natürlich t. Außerdem können wir das „ + C “ weglassen. Die so ermittelte Stammfunktion 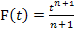schreiben wir in eckige Klammern, wobei die Grenzen an die rechte Klammer geschrieben werden. In einem zweiten Schritt werden dann die Grenzen für t eingesetzt:Zuerst die obere, dann minus die untere.

Zu 1a.)

Hier noch einmal die angegebene Integralfunktion: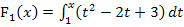

1. Schritt:Integrieren, also Stammfunktion ermitteln

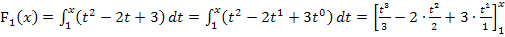
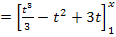
2. Schritt:Grenzen einsetzen

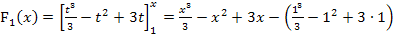
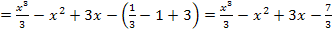
Fertig!

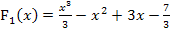ist die gesuchte integralfreie Darstellung der Integralfunktion .

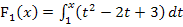Wenn du die integralfreie Darstellung von 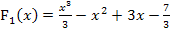mit dem Ergebnis des unbestimmten Integrals 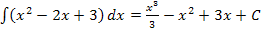vergleichst, was fällt dir dabei auf?

Das unbestimmte Integral ergibt ausgerechnet:

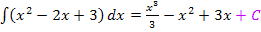
Die integralfreie Darstellung der Integralfunktion 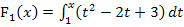ist:

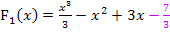
Die Zahl 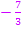bei der Integralfunktion entspricht also dem 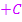beim unbestimmten Integral. Bei einer Integralfunktion ist die Integrationskonstante C somit festgelegt. Der Wert dieser Konstante hängt von der unteren Grenze ab. Das kannst du auch gleich in Teilaufgabe 1b.) erkennen. Hier ist nämlich im Vergleich zu 1a.) nur die untere Grenze verändert. Überlege dir doch gleich mal selbst, wodurch sich die integralfreien Darstellungen zweier Integralfunktionen unterscheiden, wenn nur die untere Grenze der Integralfunktionen anders ist.

Zu 1b.)

Hier noch einmal die angegebene Integralfunktion: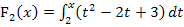

1. Schritt:Integrieren, also Stammfunktion ermitteln

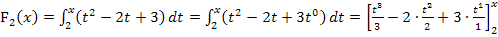
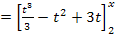
2. Schritt:Grenzen einsetzen

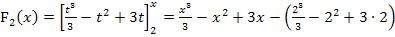
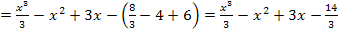
Fertig!

Die gesuchte integralfreie Darstellung von 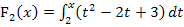lautet somit:

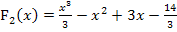
Wenn du sie mit der integralfreien Darstellung 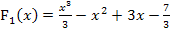der Integralfunktion 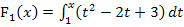vergleichst, stellst du fest, dass sie sich nur in den additiven Konstanten 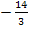und un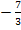terscheiden.

Es gilt generell:Zwei Integralfunktionen mit derselben Integrandenfunktion 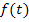aber mit unterschiedlichen unteren Grenzen 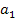und un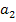terscheiden sich in ihren integralfreien Darstellungen nur in den additiven Konstanten 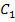und 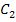. Ihre Graphen haben vom Prinzip her den gleichen Verlauf, sind aber unterschiedlich nach oben bzw. unten verschoben.

---