Polynomdivision
Dies wird mittels Polynomdivision ausgerechnet. Dadurch wird die Funktion von der angegebenen Form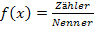 
auf die benötigte Form 
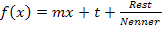gebracht. Man muss dann nur noch den letzten Teil 
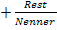weglassen und kommt so zur Gleichung der schrägen Asymptote.
Damit du das besser verstehen kannst, machen wir das einfach ´mal.
Geg.: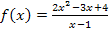 
Ges.:Gleichung der schrägen Asymptote
Polynomdivision:
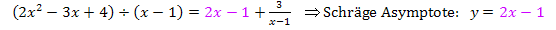
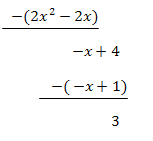
2b.) Zählergrad gleich Nennergrad
Eine gebrochenrationale Funktion mit Zählergrad gleich Nennergrad besitzt immer eine waagrechte Asymptote, die parallel zur x-Achse verläuft. (Es handelt sich dabei jedoch nicht um die x-Achse selbst. Die x-Achse ist ausschließlich dann waagrechte Asymptote, wenn der Zählergrad kleiner als der Nennergrad ist.) Wird eine gebrochenrationale Funktion betrachtet, deren Zählergrad gleich dem Nennergrad ist, wird eine Polynomdivision nur nötig, wenn die Annäherung von oben oder unten an die Asymptote untersucht werden soll.
Die Gleichung der waagrechten Asymptote kann man auch ohne weitere Rechnung an der Form 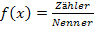an den Koeffizienten / Zahlen vor den höchsten x-Potenzen ablesen. Dazu braucht man also keine Polynomdivision!
Beispiel: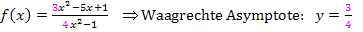 
Will man aber wissen, ob sich der Graph von oben oder von unten an die waagrechte Asymptote annähert, muss (wie schon bei der Ermittlung der schrägen Asymptote gezeigt) eine Polynomdivision durchgeführt werden. Es muss wieder der Zähler von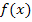 
durch den Nenner geteilt werden.
Dann betrachtet man den Restbruch und bestimmt sein Vorzeichen, natürlich in Abhängigkeit von x. Man muss also die beiden Fälle x gegen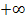 
und x gegen 
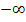getrennt untersuchen.
Ist der Restbruch größer als Null, so liegt der Funktionsgraph oberhalb der waagrechten Asymptote. Ist der Restbruch kleiner als Null, nähert sich der Funktionsgraph von unten an die waagrechte Asymptote an.
Schauen wir uns das am konkreten Beispiel an:
Nähert sich der Graph von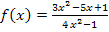 
von oben bzw. von unten an seine waagrechte Asymptote 
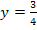an?
Polynomdivision:
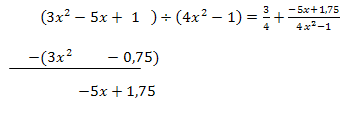
Der Ausdruck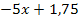 
lässt sich nicht mehr durch 
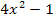teilen. Daher ist 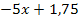der Rest. Die Polynomdivision ist schon zu Ende. Um zu beurteilen, ob sich der Graph von 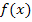nun von oben oder von unten an die waagrechte Asymptote 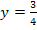annähert, betrachten wir nur noch den Term 
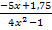. Ist er positiv oder negativ? Das hängt davon ab, ob x gegen 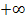oder x gegen 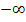geht.
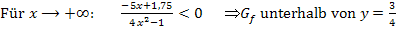
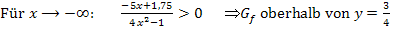
Auch bei einer Funktion mit schräger Asymptote oder asymptotischer Kurve kann danach gefragt sein, ob der Graph oberhalb oder unterhalb der schrägen Asymptote bzw. asymptotischen Kurve liegt. Die Rechnung geht entsprechend wie bei Funktionen mit waagrechter Asymptote . Den Restbruch aus der Polynomdivision auf sein Vorzeichen hin untersuchen:Ist der Restbruch positiv, liegt der Graph oberhalb der schrägen Asymptote bzw. asymptotischen Kurve. Ist der Restbruch negativ, liegt der Graph unterhalb.
Ausführlichere Erklärungen und weitere Beispiele dazu im Kapitel Kurvendiskussion gebrochenrationaler Funktionen.
