Lagebeziehungen zwischen Parabel und Gerade
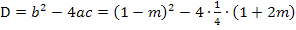
Diesen Ausdruck vereinfachen wir nun soweit möglich. Um die erste Klammer zu quadrieren, benützen wir die zweite binomische Formel: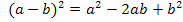 
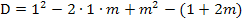
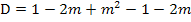
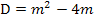
Wie oben schon erklärt, muss bei für den Fall einer Tangente gelten: D = 0
Daher setzen wir nun den oben ermittelten Ausdruck 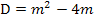gleich Null.
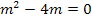
Leider liegt nun schon wieder eine gemischtquadratische Gleichung vor, also eine Gleichung mit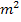 
und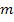 
. Man kann sie natürlich mit der Mitternachtsformel lösen. Da in diesem Fall keine Konstante (Zahl ohne m) vorhanden ist, denkt man sich einfach c = 0. Weil aber gerade die Konstante fehlt, also c = 0 gilt, lässt sich diese Gleichung viel einfacher und schneller lösen:Wir klammern m aus. Dadurch entsteht auf der linken Seite der Gleichung ein Produkt. Bekanntlich ist ein Produkt gleich Null, wenn einer der Faktoren gleich Null ist. Daher kann man dann die einzelnen Faktoren gleich Null setzen.
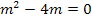
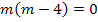
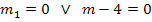
Wenn du doch den Lösungsweg mit der Mitternachtsformel bevorzugst, hier alternativ auch dieser Weg:
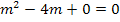
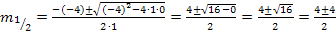
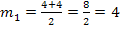
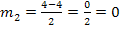
Anmerkung:Es ist Zufall, dass in diesem Aufgabenbeispiel in der letzten gemischtquadratischen Gleichung die Konstante c fehlte. Das muss nicht immer so sein! In anderen Aufgaben kann die Konstante c sehr wohl vorhanden sein. Dann muss natürlich die Mitternachtsformel verwendet werden, um die Gleichung nach dem Parameter m aufzulösen. Die Methode „Ausklammern und die Faktoren einzeln gleich Null setzen“ funktioniert dann nicht. Vielleicht hat man in einer anderen Aufgabe aber auch das Glück und es entsteht beim Nullsetzen der Diskriminante gar keine quadratische Gleichung. Dann kann ganz normal durch Umstellen nach m aufgelöst werden. Das hängt einfach von der jeweiligen Aufgabe ab. Hier wurde absichtlich ein anspruchsvolleres Beispiel gewählt.
Nun wissen wir, dass für m = 0 und für m = 4 eine Tangente vorliegt. Es existieren zwei Schargeraden, welche Tangente an die Parabel p sind. In der Aufgabe ist auch nach diesen Tangentengleichungen und dem entsprechenden Berührpunkt gefragt. Die Gleichung der Tangenten erhält man, wenn man den entsprechenden Wert (0 oder 4) für m in die Gleichung der Geradenschar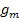 
einsetzt.
Hier noch einmal die Gleichung der Geradenschar: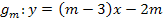 
Tangentengleichung für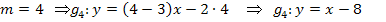 
Tangentengleichung für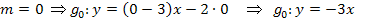 
Jetzt fehlen noch die jeweiligen Berührpunkte. Man könnte ihre x-Koordinaten berechnen, indem man einmal die Gerade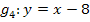 
und ein weiteres Mal die Gerade 
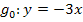mit der Parabel gleichsetzt und mit der Mitternachtsformel nach x auflöst. Das wäre jedoch sehr viel Arbeit!
