Graphische Lösungsverfahren quadratischer Gleichungen
Solltest du nicht (mehr) wissen, wie das geht, wiederhole bitte das Kapitel Berechnung des Scheitelpunkts einer Parabel! Es gibt verschiedene Methoden, wie der Scheitel berechnet werden kann. Da viele Gymnasiasten in der 9. Klassen jedoch die quadratische Ergänzung machen müssen, genau dieses Verfahren aber ziemlich aufwendig ist und daher oft zu Fehlern führt, soll es an dieser Stelle noch einmal kurz vorgeführt werden. Es werden im Folgenden zwar alle Schritte gezeigt, aber nicht näher erklärt. Sollte dir irgendetwas dabei nicht klar sein, gehe bitte in das Kapitel Quadratische Ergänzung (zur Scheitelberechnung). Dort wird das Verfahren ausführlich erläutert. Man könnte den Scheitel natürlich auch mit einer anderen Methode berechnen.
Berechnung der Scheitelkoordinaten mittels quadratischer Ergänzung:
f(x) =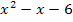 
f(x) =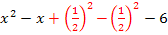 
f(x) =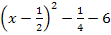 
f(x) =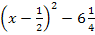 
f(x) =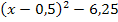 
Nun liegt die Parabel in ihrer Scheitelform vor und wir können die Koordinaten des Scheitels leicht ablesen. Der Scheitel S hat die Koordinaten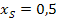 
und 
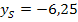. Wenn du nicht (mehr) genau weißt, wie man aus der Scheitelform den Scheitel abliest, gehe zu Scheitelform einer Parabel! Da steht, wie das funktioniert.
Nachdem wir jetzt den Scheitel S(0,5|6,25) kennen, können wir die Parabel f(x) = 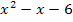direkt in ein Koordinatensystem einzeichnen. Es handelt sich schließlich um eine nach oben geöffnete Normalparabel. Daher ist eine Wertetabelle unnötig. Du musst nur den Scheitel einzeichnen und die Parabelschablone verwenden. Achte dabei allerdings darauf, dass du die Schablone wirklich genau anlegst! Wir wollen nachher schließlich die Nullstellen möglichst genau aus der Zeichnung ablesen. Versuche doch gleich mal selbst die Parabel zu zeichnen und aus der Zeichnung die Nullstellen der Parabel, also ihre Schnittpunkte mit der x-Achse, abzulesen!
Deine Zeichnung müsste so aussehen, wie die folgende Abbildung:
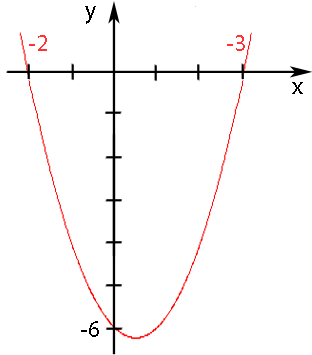
Abb.: Graph der Funktion f(x) = 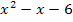Eine Normalparabel mit dem Scheitel S(0,5|-6,25) und den Nullstellen 
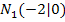und 
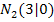
Aus der Zeichnung lassen sich nun die Nullstellen, also die Schnittpunkte mit der x-Achse ablesen. Die x-Koordinaten der Nullstellen sind die Lösungen unserer quadratischen Gleichung. Da es zwei Nullstellen gibt, gibt es auch zwei Lösungen: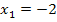 
und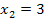 
Daher ist die gesuchte Lösungsmenge L =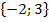 
Damit haben wir die Aufgabe gelöst. In diesem Aufgabenbeispiel existierten zwei verschiedene Lösungen. Das ist nicht bei jeder quadratischen Gleichung der Fall. Dies zeigen die folgenden beiden Beispiele.
