Grenzwerte von e- und ln-Funktionen

Ermittlung der maximalen Definitionsmenge :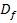

Der Ausdruck 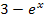, der im Nenner unter der Wurzel steht, muss positiv sein;ansonsten wäre die Funktion nicht definiert. Dass der Ausdruck unter einer Wurzel, der sogenannte Radikand, nicht negativ sein darf, ist dir bestimmt klar:Aus negativen Zahlen kann man die Wurzel nicht ziehen. Warum darf  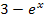hier aber auch nicht gleich Null sein? Aus der Zahl Null ließe sich zwar die Wurzel ziehen, aber wegen 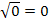würde der Nenner der Funktion gleich Null werden. Die Division durch Null ist aber nicht definiert. Daher muss gelten:

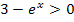
Jetzt müssen wir die vorliegende Ungleichung nach x auflösen. Im Prinzip löst man Ungleichungen genauso wie Gleichungen, nur dass man darauf achten muss, wann sich das Ungleichheitszeichen umdreht:Bei der Multiplikation mit einer negativen Zahl und bei der Division durch eine negative Zahl dreht sich das Ungleichheitszeichen um! (Siehe auch:Inversionsgesetz)

Das Ungleichheitszeichen dreht sich aber nicht um, wenn man auf beiden Seiten einer Ungleichung eine Funktion anwendet, die streng monoton steigend ist. Logarithmiert man eine Ungleichung auf beiden Seiten, ändert sich daher nichts am Ungleichheitszeichen, weil die Logarithmus-Funktion streng monoton steigend ist. Du kannst also bei Ungleichungen getrost den ln auf beiden Seiten anwenden, ohne dass du am Ungleichheitszeichen etwas ändern musst! Das Ungleichheitszeichen bleibt dabei, wie es vorher war. (Entsprechendes gilt für die Anwendung von 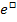bei Ungleichungen, denn auch die e-Funktion ist streng monoton steigend. Wenn du also einmal einen ln in einer Ungleichung beseitigen willst, kannst du ruhig auf beiden Seiten der Ungleichung 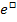rechnen;das Ungleichheitszeichen bleibt davon unberührt.)

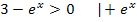
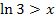
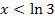
Die gesuchte Definitionsmenge lautet somit: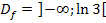

Verhalten von 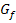an den Rändern von :

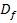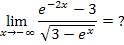
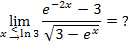
Anmerkung:Verlangt ist in der Aufgabe, dass man „das Verhalten von 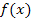an den Rändern der Definitionsmenge“ untersucht. Zu den Rändern der Definitionsmenge zählen logischerweise der linke und der rechte Rand, also die kleinste bzw. größte Zahl, die man gerade noch einsetzen kann oder gerade nicht mehr einsetzen kann, aber auch eventuell vorhandene Definitionslücken.

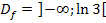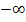Der linke Rand der Definitionsmenge ist ;der rechte Rand von 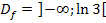ist ln3. Etwaige Definitionslücken gibt es hier nicht. Wir müssen also den Grenzwert von 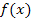für 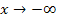berechnen und den für  . Das Kleiner-Zeichen deutet dabei an, dass wir uns von links an die Stelle ln3 annähern. Nur links von ln3, also für x <ln3, ist die Funktion 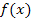überhaupt definiert. Deshalb nähern wir uns an die Stelle ln3 nur von links an und nicht von rechts. (Rechts von ln3, also für x >ln3 ist 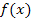ja gar nicht definiert. Der rechtsseitige Grenzwert existiert folglich gar nicht.)

---