Grenzwerte von e- und ln-Funktionen

a.)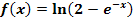

b.)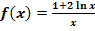

Lösung:

Zu 6a.)

Geg.: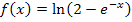

Wir ermitteln zuerst die Definitionsmenge. Die ln-Funktion y = lnx ist nur für positive Argumente x definiert. (Das „Argument des ln“ ist immer der Ausdruck, auf den sich der ln bezieht, also das, was direkt hinter dem ln steht.) Das Argument des ln muss also positiv sein. In diesem Fall ist das Argument des ln der Term 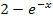;dieser Ausdruck muss positiv sein, damit der ln definiert ist. Es muss gelten:

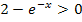
Diese Ungleichung müssen wir nach x auflösen.

Vorsicht:Das Ungleichheitszeichen dreht sich um, wenn man die Ungleichung auf beiden Seiten mit einer negativen Zahl multipliziert oder durch eine negative Zahl dividiert!

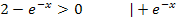
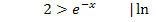
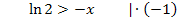
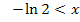
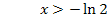
Die Definitionsmenge lautet daher: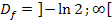

Die Ränder der Definitionsmenge liegen also bei – ln2 und bei 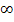. An die Stelle – ln2 können wir uns nur von rechts annähern, weil die Funktion nur für x > – ln2 definiert ist. Wir müssen also die folgenden beiden Grenzwerte ermitteln:

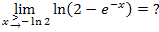
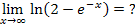
Wir beginnen mit dem linken Rand der Definitionsmenge, also mit dem rechtsseitigen Grenzwert an der Stelle – ln2:

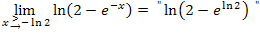
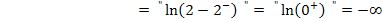
Du kannst das auch folgendermaßen schreiben:

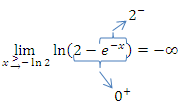
Senkrechte Asymptote:

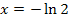
Nun zum Verhalten im Unendlichen:

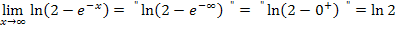
Oder in der anderen Schreibweise:

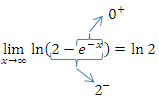
Waagrechte Asymptote: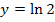 

Der Graph nähert sich von unten an seine waagrechte Asymptote y = ln2 an. Das erkennt man daran, dass von der Zahl 2, die innerhalb der Klammer hinter dem ln steht, immer noch 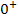subtrahiert, also ein klein wenig abgezogen wird. Es hat sich schließlich 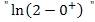ergeben.

Damit du dir das Ganze besser vorstellen kannst, hier noch zusätzlich der Graph der Funktion zusammen mit seinen Asymptoten. (Die Zeichnung war an sich in der Aufgabe nicht verlangt.)

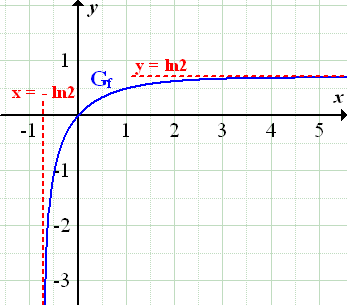
Abb.:Der Graph 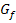der Funktion 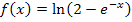in Blau und seine Asymptoten (rot gestichelt)

Zu 6b.)

Geg.: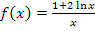

Das Argument x darf bei 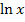nicht negativ oder gleich Null sein. (Das „Argument“ des ln ist das, was direkt hinter dem ln steht, also das, worauf sich der ln bezieht.) x muss daher größer als Null sein. Auch der Nenner darf nicht gleich Null werden. Der Nenner würde hier aber nur gleich Null werden, wenn man x = 0 wählt. Doch x = 0 ist ja schon wegen lnx nicht zugelassen. Die Funktion ist somit für beliebige positive Werte von x definiert.

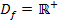
Statt 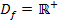könnte man auch 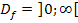schreiben. Daran sind die Ränder der Definitionsmenge leicht zu erkennen. Der linke Rand ist offensichtlich x = 0, der rechte Rand ist Unendlich. An die Stelle x = 0 kann man sich nur von rechts annähern, weil die Funktion schließlich bloßfür x >0 definiert ist. Wir müssen also den rechtsseitigen Grenzwert an der Stelle 0 berechnen und den Grenzwert für x gegen Unendlichen.

---