Grenzwerte von e- und ln-Funktionen

1. Methode:Nur mit Überlegung, ohne konkrete Rechnung

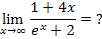
Notwendige Vorüberlegungen:

Bei 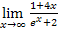geht der Zähler 1 + 4x offensichtlich gegen Unendlich. Es gilt schließlich: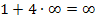

Der Nenner 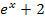geht für ebenfalls gegen Unendlich wegen .

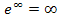Zähler und Nenner gehen also beide gegen Unendlich. Die e-Funktion im Nenner wächst allerdings schneller als das Polynom im Zähler, die e-Funktion überwiegt. Das Unendlich im Nenner ist quasi größer als das Unendlich im Zähler. Eine kleinere Zahl durch eine sehr viel größere Zahl geteilt, ergibt etwas sehr kleines, also fast Null.

Für den gesuchten Grenzwert gilt deswegen:

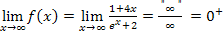
Begründung:Der Nenner wächst schneller als der Zähler.

Diese Begründung musst du unbedingt hinschreiben!

2. Methode:Verwendung bekannter Grenzwerte

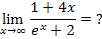
Man formt die Funktion 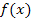so um, dass man letztendlich auf den bekannten Grenzwert 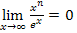kommt.

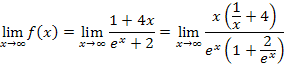
Wegen 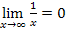und 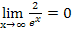ergibt sich:

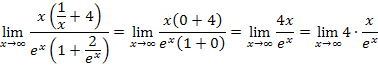
Unter Verwendung des bekannten Grenzwerts 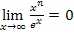erhält man:

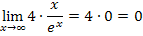
Das Vorzeichen der Null muss man sich extra überlegen;das kann nicht mit Hilfe des bekannten Grenzwertes geschehen, sondern nur mit den normalen Vorzeichenregeln der Division.

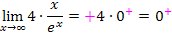
Hinweis:Es gilt 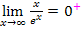, weil x für positiv ist und sowieso immer positiv ist. Plus durch Plus ist natürlich Plus.

3. Methode:Berechnung des Grenzwertes mit der Regel von L´Hospital

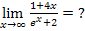
Für geht sowohl der Zähler gegen 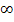als auch der Nenner. Es ergibt sich damit ein Ausdruck der Form .

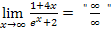
Es liegt ein Ausdruck der Form vor, wir dürfen daher die Regel von L´Hospital anwenden.

Unabhängig von der gewählten Methode kommt natürlich immer das gleiche Ergebnis heraus:

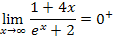
Aber was bedeutet dieses Ergebnis anschaulich? Die Funktion 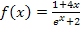hat für eine waagrechte Asymptote. Diese Asymptote hat die Gleichung y = 0;der Graph 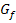hat also die x-Achse für als waagrechte Asymptote. nähert sich für von oben an die x-Achse an. (Das erkennt man an dem positiven Vorzeichen der Null.) Für 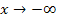gilt diese Asymptote nicht. Das erkennt man an dem zweiten ermittelten Grenzwert.

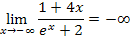
Für 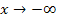geht die Funktion 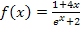gegen Minus-Unendlich. D.h. ihr Graph schießt im Koordinatensystem relativ steil nach links unten. Damit du dir das besser vorstellen kannst, hier der Graph der Funktion.

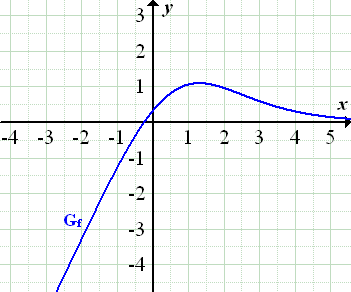
Abb.:Graph der Funktion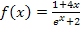

4. Bsp.:

Wir betrachten die Funktion 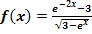. Ermittle die maximale Definitionsmenge und untersuche das Verhalten von an den Rändern der Definitionsmenge! Gib auch die Gleichungen aller Asymptoten an!

Lösung:

Geg.: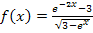

Ges.: 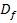und Verhalten an den Rändern von 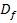(einschließlich aller Asymptoten)

---