Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
Auch kein Randpunkt kann somit Maximum sein. Damit ist sichergestellt, dass sich für x = 1 wirklich der absolut größte Flächeninhalt des Dreiecks ergibt. Die Randpunktuntersuchung (6. Schritt) entfällt.
Wir müssen noch die y-Koordinate des Punktes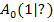 
und den maximalen Flächeninhalt des Dreiecks 
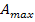berechnen. Die y-Koordinate von 
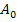bekommen wir, wenn wir seine x-Koordinate x = 1 in die Funktion 
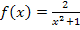einsetzen, weil ja alle Punkte 
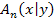auf der Funktion 
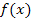liegen.
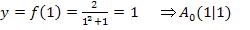
Den maximalen Flächeninhalt des Dreiecks 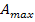erhält man, indem man x = 1 in die Zielfunktion 
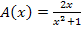einsetzt.
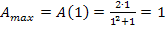
Dass sich für die x-Koordinate und für die y-Koordinate von 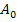sowie für 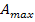jeweils der gleiche Wert, nämlich 1 ergibt, ist reiner Zufall.
Nun fehlen nur noch die Koordinaten des Eckpunktes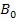 
. Man kann sie sich leicht anschaulich herleiten. Sowohl 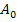als auch 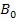liegen auf der zur y-Achse symmetrischen Funktion 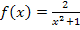. 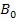ergibt sich durch Spiegelung von 
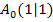an der y-Achse. Vergleiche dazu die oben gezeigte Abbildung! 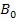hat die selbe y-Koordinate wie 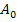, aber eine vom Vorzeichen her umgekehrte x-Koordinate. Daher muss gelten: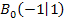 
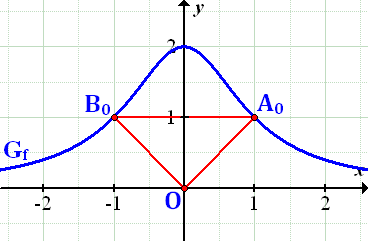
Hier kannst du das Dreieck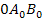 
für 
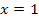sehen. (Die Zeichnung war eigentlich nicht verlangt.)
So, nun zu einem etwas schwereren Beispiel, das aber in fast keinem Mathebuch zum Thema Extremwertaufgaben/Optimierungsprobleme fehlt.
4. Bsp.:Die optimale Dose
Eine zylindrische Dose soll ein Volumen von 0,33 Liter haben. Wie müssen bei dieser Dose Radius und Höhe gewählt werden, so dass sich der kleinstmögliche Materialverbrauch, d.h. Oberflächeninhalt ergibt. Wie großist dieser minimale Oberflächeninhalt?
Lösung:
Bezeichnung der Variablen festlegen:
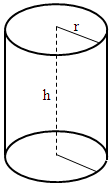
Der Radius der zylindrischen Dose wird mit r bezeichnet und die Höhe mit h. Als Einheit wählen wir jeweils cm.
Radius des Zylinders in 
:r
Höhe des Zylinders in 
:h
Wir machen uns erst mal eine Skizze.
1. Schritt:Nebenbedingung aufschreiben
Das Volumen der zylindrischen Dose soll 0,33 l betragen. Zu der Volumeneinheit Liter gibt es keine zugehörige Längeneinheit. Daher rechnen wir von der Einheit Liter in eine andere Volumeneinheit um, zu der es eine Längeneinheit gibt. Man kann entweder in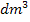 
oder in 
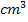umwandeln. 1 Liter entspricht einem 1 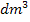oder 1000 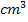. Da wir vorher festgelegt haben, dass sowohl der Radius r als auch die Höhe h in berechnet werden sollen, müssen wir von Liter in 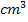umrechnen.
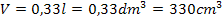
In der Formelsammlung bzw.
