Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren
Damit du einen Funktionsterm aufstellen kannst, brauchst du als erstes natürlich einen allgemeinen Ansatz. In den meisten Aufgaben ist dieser nicht angegeben;du musst ihn dir dann selbst überlegen. Der benötigte allgemeine Ansatz hängt logischerweise davon ab, was für eine Funktion gesucht ist, ob z.B. eine Polynomfunktion 3. Grades oder 4. Grades gesucht ist, oder ob die Funktion vielleicht eine Symmetrie zum Koordinatensystem aufweist. (Punktsymmetrisch zum Ursprung oder Achsensymmetrisch zur y-Achse. Mehr dazu bei Symmetrieverhalten) Die wichtigsten Ansätze findest du in der Tabelle Nr. 2.
Manchmal sind auch verschiedene Ansätze möglich, zum Beispiel für ein Polynom dritten Grades der „normale“ Ansatz 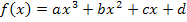 und der in der faktorisierten Form, d.h. Produktform
und der in der faktorisierten Form, d.h. Produktform 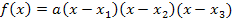 . Dabei stellen
. Dabei stellen 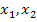 und
und 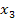 die Nullstellen der Funktion dar. Sind bei einer Polynomfunktion n.-ten Grades alle n Nullstellen bekannt, lässt sich der Funktionsterm mit Hilfe der faktorisierten Form wesentlich schneller aufstellen als mit dem „normalen“ Ansatz. Das funktioniert aber nur dann, wenn wirklich alle n Nullstellen gegeben sind. (Der Buchstabe n steht hier für eine natürliche Zahl, also zum Beispiel für die Zahl 3.) Denke daran, dass eine Polynomfunktion n.-ten Grades höchstes n verschiedene Nullstellen besitzen kann.
die Nullstellen der Funktion dar. Sind bei einer Polynomfunktion n.-ten Grades alle n Nullstellen bekannt, lässt sich der Funktionsterm mit Hilfe der faktorisierten Form wesentlich schneller aufstellen als mit dem „normalen“ Ansatz. Das funktioniert aber nur dann, wenn wirklich alle n Nullstellen gegeben sind. (Der Buchstabe n steht hier für eine natürliche Zahl, also zum Beispiel für die Zahl 3.) Denke daran, dass eine Polynomfunktion n.-ten Grades höchstes n verschiedene Nullstellen besitzen kann.
Ein Polynom dritten Grades kann deshalb höchstens drei Nullstellen haben. Sind also von einer Polynomfunktion dritten Grades drei verschiedene Nullstellen angegeben, weißt du, dass es keine weiteren geben kann. Es sind somit alle drei Nullstellen bekannt und man kann mit der faktorisierten Form arbeiten. Dasselbe gilt bei einem Polynom dritten Grades, wenn eine Nullstelle einfach und eine doppelt ist. Die doppelte Nullstelle betrachtest du als zwei aufeinander liegende einfache Nullstellen. Es sind dann auch alle Nullstellen gegeben und die faktorisierte Form kann verwendet werden. (Mehr zur faktorisierten Form bei Faktorisierter Funktionsterm) Der „normale“ Ansatz 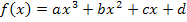 würde dabei natürlich auch zur Lösung führen, doch würde das sehr viel mehr Rechenaufwand bedeuten. Verwende deshalb immer die faktorisierte Form, wenn möglich, d.h. bei einem Polynom n.-ten Grades, wenn alle n Nullstellen gegeben sind.
würde dabei natürlich auch zur Lösung führen, doch würde das sehr viel mehr Rechenaufwand bedeuten. Verwende deshalb immer die faktorisierte Form, wenn möglich, d.h. bei einem Polynom n.-ten Grades, wenn alle n Nullstellen gegeben sind.
Tabelle Nr. 2
| Art der gesuchten Funktion | Allgemeiner Ansatz |
| Polynomfunktion 2. Grades
Andere Formulierung: Quadratische Funktion oder Parabel oder ganzrationale Funktion zweiten Grades |
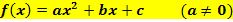
Oder in Scheitelform:
Scheitelform nur verwenden, wenn der Scheitel Oder in faktorisierter Form:
Faktorisierte Form nur verwenden, wenn beide Nullstellen |
|
Polynomfunktion 3. Grades Andere Formulierung: Ganzrationale Funktion 3. Grades |
Oder in faktorisierter Form: Wenn
Wenn
Wenn
|
| Polynomfunktion 3. Grades, die punktsymmetrisch zum Ursprung ist
Andere Formulierung: Ganzrationale Funktion 3. Grades, die punktsymmetrisch zum Ursprung ist |
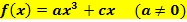
Erklärung: Es treten nur ungerade Potenzen von x auf. Daher sind alle Koeffizienten, die im allgemeinen Ansatz eines Polynoms dritten Grades
vor geraden x-Potenzen stehen gleich Null:
So ergibt sich der oben gezeigte vereinfachte Ansatz:
|
| Polynomfunktion 4. Grades
Andere Formulierung: Ganzrationale Funktion 4. Grades |
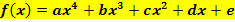
Oder in faktorisierter Form: Wenn
Wenn
Wenn
|
| Polynomfunktion 4. Grades, die achsensymmetrisch zur y-Achse ist
Andere Formulierung: Ganzrationale Funktion 4. Grades, die achsensymmetrisch zur y-Achse ist |
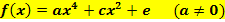
Erklärung: Es treten nur gerade Potenzen von x auf. Daher sind alle Koeffizienten, die im allgemeinen Ansatz eines Polynoms vierten Grades
vor ungeraden x-Potenzen stehen gleich Null:
So ergibt sich der oben gezeigte vereinfachte Ansatz:
|
| Polynomfunktion 5. Grades
Andere Formulierung: Ganzrationale Funktion 5. Grades |
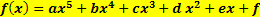
Die faktorisierte Form wird statt des gezeigten Ansatzes verwendet, wenn fünf verschiedene (einfache) Nullstellen gegeben sind, bzw. wenn die Vielfachheiten der Nullstellen zusammen fünf ergibt, z. B. eine einfache und zwei doppelte Nullstellen oder eine doppelte und eine dreifache Nullstelle. Da es hierfür sehr viele Möglichkeiten gibt, können hier nicht alle denkbaren Ansätze aufgeführt werden. |
| Polynomfunktion 5. Grades, die punktsymmetrisch zum Ursprung ist
Andere Formulierung: Ganzrationale Funktion 5. Grades, die punktsymmetrisch zum Ursprung ist |
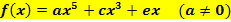
Erklärung: Es treten nur ungerade Potenzen von x auf. Daher sind alle Koeffizienten, die im allgemeinen Ansatz eines Polynoms fünften Grades
vor geraden x-Potenzen stehen gleich Null:
So ergibt sich der oben gezeigte vereinfachte Ansatz:
|
Nun versuche dich gleich an dem nächsten Beispiel! Den korrekten Ansatz und die nötigen Informationen kannst du mit Hilfe der oben gezeigten Tabellen nun sicher selbst finden. Also erst mal alleine versuchen, dann die Lösung anschauen!

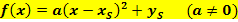
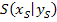 gegeben ist
gegeben ist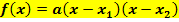
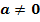
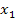 und
und 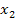 bekannt sind
bekannt sind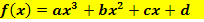
 drei einfachen Nullstellen
drei einfachen Nullstellen 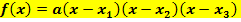
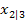 hat und diese Nullstellen beide bekannt sind, folgenden Ansatz wählen:
hat und diese Nullstellen beide bekannt sind, folgenden Ansatz wählen: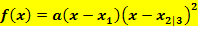
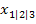 hat und diese Nullstellen beide bekannt sind, folgenden Ansatz wählen:
hat und diese Nullstellen beide bekannt sind, folgenden Ansatz wählen: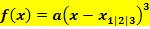
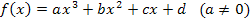

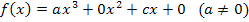
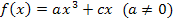
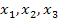 und
und 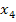 hat und alle Nullstellen gegeben sind, folgenden Ansatz wählen:
hat und alle Nullstellen gegeben sind, folgenden Ansatz wählen: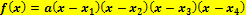
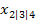 hat und diese Nullstellen beide bekannt sind, folgenden Ansatz wählen:
hat und diese Nullstellen beide bekannt sind, folgenden Ansatz wählen: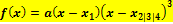
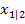 und
und 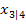 hat und diese Nullstellen beide bekannt sind, folgenden Ansatz wählen:
hat und diese Nullstellen beide bekannt sind, folgenden Ansatz wählen: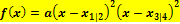
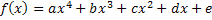
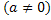

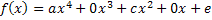
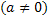
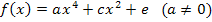
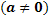
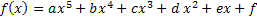
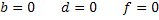
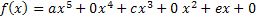
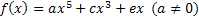 .
.