Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren
Bisher war eine Funktionsgleichung 
gegeben und man sollte die Nullstellen, die Extrema (Hochpunkte und Tiefpunkte) und die Wendepunkte im Rahmen einer Kurvendiskussion soweit vorhanden berechnen. Nun wollen wir uns dem umgekehrten Problem widmen. Wie findet man die Funktionsgleichung, wenn einige bestimmte Kurvenpunkte, wie zum Beispiel Nullstellen, Extrema und Wendepunkte, oder die Steigung in bestimmten Kurvenpunkten gegeben sind?
Einführungsbeispiel:
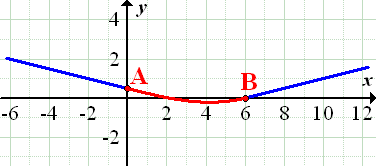
Es soll eine Verbindungsstraße zwischen zwei geradlinigen Straßen gebaut werden. Siehe Skizze! Die Kurve (in der Skizze rot gezeichnet) soll dabei „weich“ verlaufen, also ohne Knick die eine Straße mit der anderen verbinden. Welche Gleichung muss eine Polynomfunktion dritten Grades haben, die den Kurvenverlauf beschreibt?
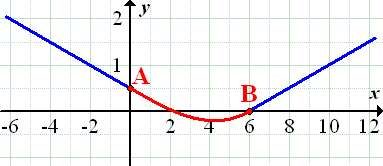
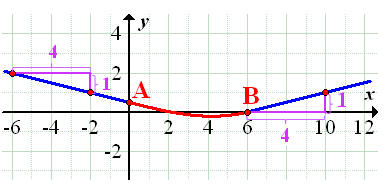
Abb.:Zwei Straßen (in Aufsicht), die zwischen den Punkten A und B weich durch eine Kurve (rot dargestellt) verbunden werden sollen
Lösung:
Der Zeichnung können wir entnehmen:Die fallende, d.h. linke Gerade endet im Punkt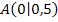 
. Der Punkt A hat leider keine ganzzahligen Koordinaten. Um ein Steigungsdreieck an die linke Gerade zu zeichnen, verwenden wir daher besser zwei andere Punkte. Wir lesen deshalb aus der Zeichnung zusätzlich zwei beliebige Punkte der linken Geraden ab, deren Koordinaten ganzzahlig sind. Nehmen wir beispielsweise die Punkte 
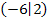und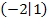 
. Die Steigung der linken Geraden lässt sich mit Hilfe eines Steigungsdreiecks zwischen diesen beiden Punkten gut ablesen. Sie hat die Steigung 
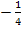. (Vier nach rechts und Eins nach unten;beachte dabei den unterschiedlichen Maßstab auf den beiden Achsen in der Abbildung oben! Auf der x-Achse gilt:1 Kästchen 
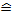1 LE Auf der y-Achse gilt:1 Kästchen 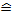0.5 LE) Du hättest das Steigungsdreieck natürlich auch zwischen zwei anderen Punkten zeichnen können, z.B. von 
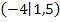zu 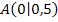. Aber zwischen Punkten mit ganzzahligen Koordinaten lässt sich die Steigung der Geraden etwas einfacher ablesen.
In der folgenden Abbildung kannst du sehen, wie das Ganze aussieht, wenn auf beiden Achsen der gleiche Maßstab 1 Kästchen 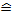1 LE gewählt wird.
Die steigende, d.h. rechte Gerade beginnt im Punkt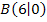 
. Der Punkt B hat ganzzahlige Koordinaten, von B ausgehend lässt sich schön ein Steigungsdreieck an die rechte Gerade zeichnen. Nun suchen wir uns einen weiteren Punkt, der ebenfalls auf der rechten Geraden liegt und von dem sich die Koordinaten gut ablesen lassen. Wir entscheiden uns für den Punkt 
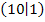. Zeichnet man zwischen den Punkten 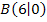und 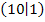ein Steigungsdreieck, kann man leicht die Steigung dieser Geraden ablesen. Sie beträgt 
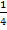. (Vier nach rechts und Eins nach oben) Mit der folgenden Abbildung müsste dir das hoffentlich klar werden.
Es soll eine Polynomfunktion dritten Grades gefunden werden, welche die beiden Geraden ohne Knick, also in einer weichen Kurve, miteinander verbindet.
Hinweis:Der Grad eines Polynoms ist die höchste vorkommende Potenz von x.
Ansatz für eine Polynomfunktion 3. Grades: 
Es müssen die Formvariablen a, b, c und d berechnet werden;dann lässt sich die Funktion leicht aufstellen.
