Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren
Bei einem Extremum verläuft die Tangente waagrecht, d.h. die Steigung ist dort gleich Null. Da die erste Ableitung der Steigung entspricht, gilt:
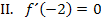
Dritte Information:Bei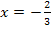 
hat der Graph einen Wendepunkt. Wendepunkte berechnet man bekanntlich mit dem Ansatz 
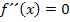, da sich im Wendepunkt das Krümmungsverhalten, also das Vorzeichen der zweiten Ableitung ändert. Die zweite Ableitung entspricht schließlich der Krümmung des Graphen. Daher gilt:
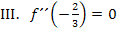
Mit Hilfe der drei Informationen lassen sich die drei benötigten Gleichungen aufstellen.
Hier noch einmal die Funktionsgleichung und ihre ersten zwei Ableitungen in der allgemeinen Form:
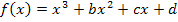
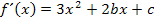
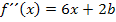
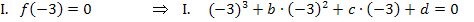
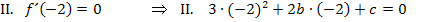
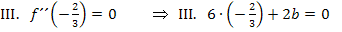
Wir vereinfachen die drei Gleichungen erst einmal.
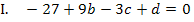
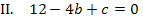
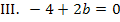
Dieses Gleichungssystem lässt sich ganz besonders leicht lösen, denn III. enthält nur die Unbekannte b. Wir lösen III. einfach nach b auf.
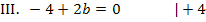
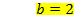
Jetzt setzen wir b in II. ein. Da die Gleichung II. nur die Unbekannten b und c enthält, kann c nach dem Einsetzen von b ganz leicht durch bloßes Umstellen ermittelt werden.
b in II.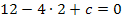 
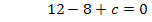
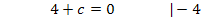
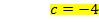
Wie es jetzt weiter geht, dürfte klar sein:Einfach die ermittelten Werte für b und c in I. einsetzen und nach der verbliebenen Unbekannten d auflösen.
Hier noch einmal Gleichung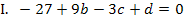 
b und c in I.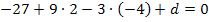 
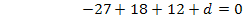
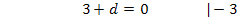
Nun kennen wir alle drei Unbekannten: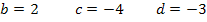 
Wir brauchen sie nur noch in 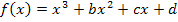einzusetzen. Das ergibt:
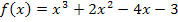
Damit ist die Aufgabe gelöst. Hier noch der Graph der Funktion .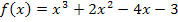
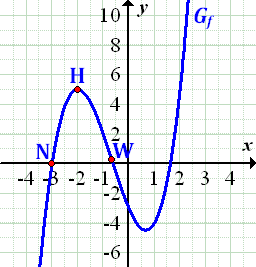
Abb.:Graph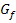 
der zu ermittelnden Funktion 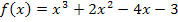;rot markiert sind die ursprünglich angegebenen Punkte:Nullstelle N bei x = -3, Hochpunkt H bei x = -2 und Wendepunkt W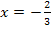
Im soeben vorgeführten Beispiel war das Gleichungssystem, welches benötigt wurde, um die Funktionsgleichung von 
zu finden, noch sehr leicht lösbar. Das ist natürlich nicht bei allen Aufgaben dieses Typs der Fall. Auch lassen sich die benötigten Informationen nicht immer so leicht aus der Angabe entnehmen. Manchmal sind einige Informationen etwas versteckt, beispielsweise in der Angabe der x-Koordinate eines Wendepunktes und der zugehörigen Gleichung der Wendetangente. Welche Informationen sich dahinter verbergen, schauen wir uns im nächsten Beispiel an.
2. Bsp.:
Gesucht ist die Gleichung einer ganzrationalen Funktion dritten Grades, deren Graph bei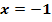 
die x-Achse schneidet und bei 
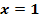einen Wendepunkt mit der Wendetangente 
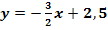besitzt.
Lösung:
Eine ganzrationale Funktion dritten Grades ist das gleiche wie eine Polynomfunktion dritten Grades.
