1. Flächenberechnungenmit Hilfe von Integralen
Du musst also immer nach dem Buchstaben integrieren, der innerhalb der Klammer direkt hinter der Funktionsbezeichnung steht. Dieser Buchstabe ist die Variable. Nur bei den Exponenten dieses Buchstabens musst du 1 dazuzählen und dann auch noch durch den neuen Exponenten teilen. Alle anderen Buchstaben (es könnten auch mehrere Scharparameter auftreten) behandelst du wie ganz normale Zahlen.
Du hättest wahrscheinlich automatisch nach x integriert und somit bei dieser Aufgabe nach dem richtigen Buchstaben integriert. Aber Vorsicht:Das ist eben nicht bei allen Aufgaben so. Wäre beispielsweise die Funktionenschar 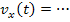 gegeben, müsste nach t integriert werden, weil t dabei die Variable darstellt. Der Buchstabe t steht innerhalb der Klammer hinter der Funktionsbezeichnung
gegeben, müsste nach t integriert werden, weil t dabei die Variable darstellt. Der Buchstabe t steht innerhalb der Klammer hinter der Funktionsbezeichnung 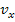 ;daher ist t dabei die Variable. Dagegen wäre x bei
;daher ist t dabei die Variable. Dagegen wäre x bei 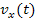 bloßder Scharparameter und nicht wie normal die Variable! Du müsstest dann dt hinter das Integral schreiben und dich beim Integrieren nur auf die Potenzen von t konzentrieren, also nur bei den Exponenten von t die Zahl 1 dazuzählen usw. Das x müsstest du dabei als feste Zahl behandeln.
bloßder Scharparameter und nicht wie normal die Variable! Du müsstest dann dt hinter das Integral schreiben und dich beim Integrieren nur auf die Potenzen von t konzentrieren, also nur bei den Exponenten von t die Zahl 1 dazuzählen usw. Das x müsstest du dabei als feste Zahl behandeln.
Nun aber wieder zurück zu unserer Aufgabe. Wir müssen 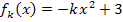 von 0 bis
von 0 bis 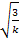 nach x integrieren.
nach x integrieren.
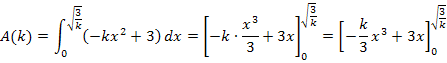
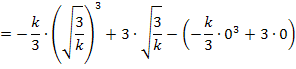
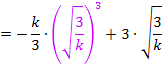
Den vorliegenden Ausdruck müssen wir noch vereinfachen. Wir müssen dazu den Term 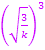 ausrechnen. Das machen wir in einer Nebenrechnung:
ausrechnen. Das machen wir in einer Nebenrechnung:
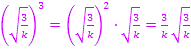
Damit ergibt sich für den Flächeninhalt in Abhängigkeit von k:
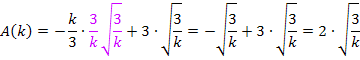
Gesucht ist derjenige Wert von k, für den sich der Flächeninhalt 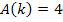 ergibt. Wir setzen daher für
ergibt. Wir setzen daher für 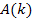 nun den Wert 4 ein. So erhalten wir die folgende Gleichung:
nun den Wert 4 ein. So erhalten wir die folgende Gleichung:
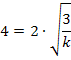
Wir müssen diese Gleichung nur noch nach k auflösen. Dann sind wir fertig.
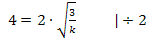
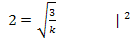


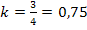
Für 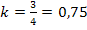 ergibt sich der geforderte Flächeninhalt von 4 FE zwischen Funktionsgraph und den Koordinatenachsen, das im I. Quadranten liegt.
ergibt sich der geforderte Flächeninhalt von 4 FE zwischen Funktionsgraph und den Koordinatenachsen, das im I. Quadranten liegt.
6. Bsp.:Extremaler Flächeninhalt und zugehöriger Scharparameter gesucht
Gegeben ist die Funktionenschar 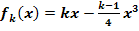 mit k >1. Die Graphen werden mit
mit k >1. Die Graphen werden mit 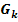 bezeichnet.
bezeichnet.
Der Graph 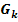 schließt für k >1 mit der positiven x-Achse ein Flächenstück ein. Berechne den Inhalt
schließt für k >1 mit der positiven x-Achse ein Flächenstück ein. Berechne den Inhalt 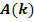 dieses Flächenstücks in Abhängigkeit von k. Ermittle sodann denjenigen Wert von k, für den
dieses Flächenstücks in Abhängigkeit von k. Ermittle sodann denjenigen Wert von k, für den 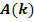 minimal bzw. maximal wird. Überprüfe rechnerisch, ob die Fläche dann am größten oder am kleinsten ist. Wie großist dieser Flächeninhalt?
minimal bzw. maximal wird. Überprüfe rechnerisch, ob die Fläche dann am größten oder am kleinsten ist. Wie großist dieser Flächeninhalt?
Lösung:
Gesucht ist als erstes die Fläche zwischen einem der Graphen der Schar 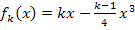 mit k >1 und der (positiven) x-Achse.
mit k >1 und der (positiven) x-Achse.
Die Angabe k >1 ist sehr wichtig! Wäre nämlich bezüglich k nichts angegeben gewesen, hätte k  ℝ gegolten und wir müssten nachher eine Fallunterscheidung machen. (Für k = 1 gäbe es gar keine solche Fläche, weil
ℝ gegolten und wir müssten nachher eine Fallunterscheidung machen. (Für k = 1 gäbe es gar keine solche Fläche, weil 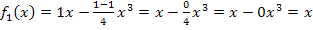 die Gleichung der Winkelhalbierenden ist. Die Winkelhalbierende schließt aber mit der x-Achse überhaupt kein Flächenstück ein. Für k <1 ergäbe sich ebenfalls kein Flächenstück, das durch den Graph und die x-Achse eingeschlossen wird. Das merkt man später auch daran, dass
die Gleichung der Winkelhalbierenden ist. Die Winkelhalbierende schließt aber mit der x-Achse überhaupt kein Flächenstück ein. Für k <1 ergäbe sich ebenfalls kein Flächenstück, das durch den Graph und die x-Achse eingeschlossen wird. Das merkt man später auch daran, dass 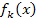 nur für k >1 mehrere Nullstellen hat. Darauf wird weiter unten bei der Nullstellenberechnung noch genauer eingegangen.)
nur für k >1 mehrere Nullstellen hat. Darauf wird weiter unten bei der Nullstellenberechnung noch genauer eingegangen.)

