Das bestimmte und das unbestimmte Integral

Diese beiden Integrale lassen sich daher nicht zu einem Integral zusammenfassen. Sie müssen einzeln berechnet und die Ergebnisse dann voneinander abgezogen werden.

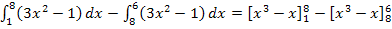
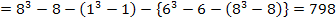
Erwähnt werden soll noch eine weitere Formel, die man gelegentlich brauchen kann:

Die sogenannte Faktor-Formel besagt:

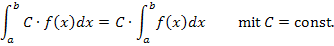
Die Faktor-Formel besagt eigentlich nichts anderes, als dass man multiplikative Konstanten (d.h. Zahlen ohne x, die mit etwas multipliziert werden) vor das Integral ziehen darf. Das gilt jedoch nicht bei Ausdrücken, welche die Variable x enthalten! Ein Ausdruck mit x darf niemals vor das Integral gezogen werden!

Dass die Formel stimmt, wird dir hoffentlich am nächsten Beispiel klar.

5. Bsp.:

Berechne die folgenden beiden Ausdrücke und vergleiche die Ergebnisse!

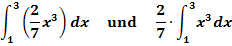
Lösung:

stellt hier die multiplikative Konstante dar. Man darf die Zahl bei 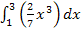vor das Integral ziehen, dann ergibt sich das zweite Integral 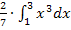. Es muss also bei beiden Integralen das gleiche herauskommen. Wir berechnen hier jedoch beide Integrale einzeln, um zu zeigen, dass gilt: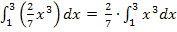

Berechnung des Integrals :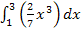

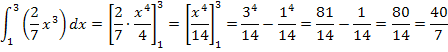
Berechnung des Integrals :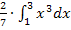

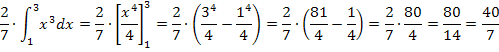
Wie erwartet stimmen die beiden Ergebnisse überein. Wir konnten somit zeigen, dass gilt:

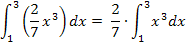
Du siehst, dass es egal ist, ob du den Bruch vor das Integral ziehst oder nicht. Es kommt immer dasselbe Ergebnis heraus.

Es ist nicht schwer, die Formel 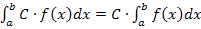allgemein zu beweisen. Versuche es doch gleich mal alleine!

Zu deiner Kontrolle hier der komplette Beweis:

Zu Zeigen: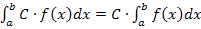

Linke Seite: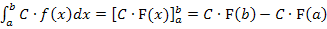

Rechte Seite: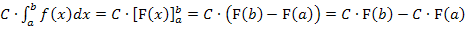

Linke und rechte Seite stimmen überein. Die Formel ist damit bewiesen.

Bei allen bisher gezeigten Beispielaufgaben musste das Ergebnis eines bestimmten Integrals ermittelt werden;die Grenzen waren dabei immer angegeben. Es gibt jedoch auch Aufgaben, bei denen eine oder sogar beide Grenzen gesucht sind. Dabei ist dann allerdings das Ergebnis des Integrals bekannt. Wie du solche Aufgaben lösen kannst, wird an Hand des nächsten Beispiels erklärt.

6. Bsp.:Grenzen gesucht

Ermittle eine reelle Zahl a so, dass gilt:

a.)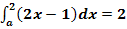

b.)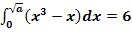

c.)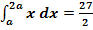

Lösung:

Um solche Aufgaben zu lösen, gehst du bei der linken Seite der Gleichung immer genauso vor, als wären die Grenzen des bestimmten Integrals bekannt. Du rechnest also das Integral auf der linken Seite der Gleichung ganz normal aus, so als wäre a eine konkrete Zahl.

Du musst dazu mit Hilfe der Formel 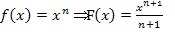eine Stammfunktion ermitteln, schreibst die Stammfunktion dann in die eckigen Klammern (Grenzen rechts daneben geschrieben) und setzt danach die Grenzen ein.

---