Das bestimmte und das unbestimmte Integral

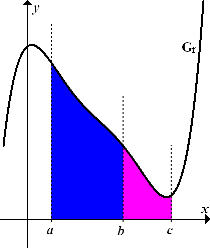
Abb.:Zur Additivität des bestimmten Integrals

Die blaue Fläche 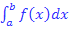plus die rosa Fläche 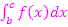ergibt die gesamte Fläche .

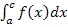Beispiel: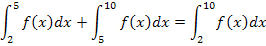

Aber Vorsicht:Das bestimmte Integral entspricht nur dann der Fläche zwischen 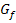und der x-Achse, wenn die Fläche oberhalb der x-Achse liegt. Die Additivität des Integrals (die oben gezeigte Formel) gilt immer, auch wenn die Fläche teilweise oder sogar komplett unterhalb der x-Achse liegt. Das Integral 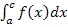entspricht dann aber nicht der gesamten Fläche zwischen Graph und x-Achse, sondern der Flächenbilanz! Das Integral 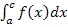ist für a <c negativ, wenn die Fläche komplett unterhalb der x-Achse liegt, aber auch dann, wenn der unterhalb der x-Achse liegende Flächenanteil größer ist als der Teil der Fläche, der oberhalb der x-Achse liegt.

Dass die Intervalladditivität des Integrals für jede beliebige Funktion gilt, lässt sich leicht beweisen. Schauen wir uns auch diesen Beweis kurz an.

Beweis der Formel :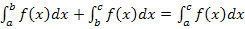

Linke Seite:

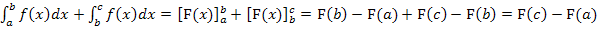
Rechte Seite:

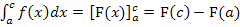
Linke und rechte Seite liefern die gleichen Ergebnisse, was wir schließlich auch zeigen wollten. Damit ist die Additivität des Integrals bewiesen.

Wofür braucht man die beiden soeben erläuterten Formeln? Das wirst du gleich am nächsten Beispiel sehen.

4. Bsp.:

Berechne die folgenden Ausdrücke, wenn möglich durch Zusammenfassen zu einem Integral!

a.)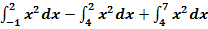

b.)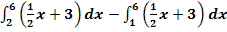

c.)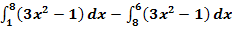

Lösung:

Zu 4a.)

Zu berechnen: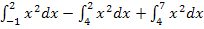

Vor dem mittleren Integral steht ein Minus. Wir vertauschen bei diesem Integral die Grenzen, dann dreht sich das Vorzeichen vor dem Integral um. Wir verwenden also beim mittleren Integral die Formel: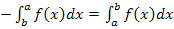

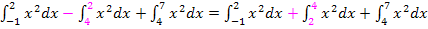
Nun erkennt man, dass die obere Grenze des ersten Integrals genau mit der unteren Grenze des zweiten übereinstimmt und die obere Grenze des zweiten Integrals genau mit der unteren Grenze des dritten. Die Integrale sollen alle addiert werden und stoßen jeweils direkt zusammen. Auf Grund der Additivität von Integralen können wir sie alle zu einem Integral zusammenfassen. Wir wenden also die Formel 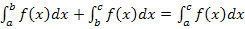an.

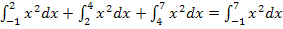
Das neue Integral lässt sich natürlich wesentlich schneller berechnen als der ursprüngliche Ausdruck.

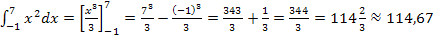
Fertig!

Zu 4b.)

Hier noch einmal die Angabe: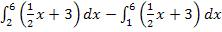

Vor dem zweiten Integral steht ein Minus. Damit man die beiden Integrale zu einem einzigen zusammenfassen kann, muss aber ein Pluszeichen vor jedem Integral stehen. Wenn wir die Grenzen des zweiten Integrals vertauschen, dreht sich das Vorzeichen bei diesem Integral um. Des Weiteren erkennt man, dass dann die beiden Integrale direkt zusammenstoßen:Nach dem Vertauschen der Grenzen beim zweiten Integral stimmt die obere Grenze des ersten Integrals mit der unteren Grenze des zweiten überein. Die beiden Integrale lassen sich wegen der Additivität von Integralen zu einem einzigen Integral zusammenfassen.

---