Das Newton-Verfahren

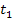Der zweite Näherungswert , also die Nullstelle der Tangente , würde genau mit dem Startwert zusammenfallen. Der dritte Näherungswert 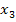würde wieder mit zusammenfallen, der vierte Näherungswert 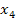mit dem Startwert usw. Der gezeigte Startwert ist somit völlig ungeeignet für die näherungsweise Berechnung der Nullstelle 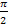der Funktion 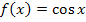mit dem Newton-Verfahren, weil sich dabei abwechselnd immer wieder die Werte 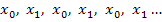ergeben würden. Eine wirkliche Annäherung an den eigentlich gesuchten Wert 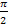findet nicht statt.

Ein extremer Sonderfall für das Versagen des Newton-Verfahrens liegt vor, wenn eine sogenannte alternierende Folge der Form 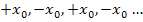entsteht. Das bedeutet, dass sich immer wieder dieselben Werte nur mit unterschiedlichen Vorzeichen ergeben. Die Werte springen quasi immer zwischen 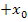und 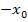hin und her, nähern sich aber nie an die tatsächliche Lösung an. Das Newton-Verfahren versagt dann natürlich wieder. Bei manchen Funktionen passiert dies nur bei ganz bestimmten Startwerten, bei anderen tritt das Problem aber für beliebige Startwerte auf. Schauen wir uns ein konkretes Beispiel dazu an.

4. Bsp.:

Das Newton-Verfahren liefert bei der Nullstellenberechnung der Funktion 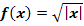für jeden von Null verschiedenen Startwert 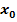eine alternierende Folge der Form 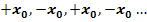Die einzige Nullstelle x = 0 kann deshalb mit dem Newton-Verfahren nicht näherungsweise berechnet werden. Erkläre diese Tatsache an Hand einer Skizze!

Lösung:

Zuerst zeichnen wir den Graph der Funktion 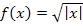beispielweise mit einer Wertetabelle. Du kannst die Funktion aber auch erst einmal betragsfrei schreiben. (Näheres zum Betrag.)

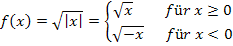
In der betragsfreien Form erkennt man, dass für 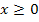die Wurzelfunktion 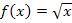gilt. Da die Wurzelfunktion die Umkehrfunktion der Normalparabel 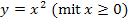ist, muss man den steigenden Ast der Normalparabel an der Winkelhalbierenden y = x spiegeln, um den Graph der Wurzelfunktion 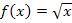zu erhalten. Für 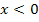gilt dagegen der zweite Teil der Funktion 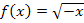. Den Graph von 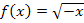erhält man durch Spiegelung des Graphen der Wurzelfunktion 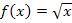an der y-Achse.

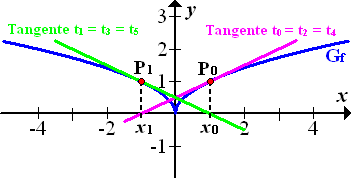
Abb.:Graph 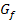der Funktion 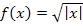mit den Tangenten in den Kurvenpunkten 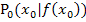und 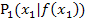, wobei gilt: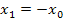

In der Abbildung ist der Graph der Funktion 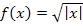dargestellt. Von einem beliebigen Startwert 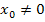geht man nun zu dem entsprechenden Kurvenpunkt 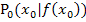auf dem Graphen.

Wählen wir beispielsweise 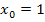, wie auch in der Abbildung gezeigt. Dann lautet der Kurvenpunkt 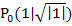, also 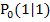. Zeichnet man in diesem Punkt die Tangente 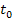und schneidet diese Tangente mit der x-Achse, erhält man den Wert .

---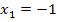