Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme

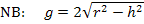
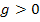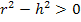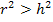Da das Ergebnis einer Wurzel immer positiv ist, wenn der Radikand (= Ausdruck unter der Wurzel) positiv ist, gilt , wenn bzw. oder 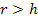. Somit muss r größer als h sein bzw. h kleiner als r sein.

Es muss also gelten: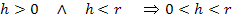 

Zu dem gleichen Ergebnis wäre man auch durch reine Überlegung an Hand der Zeichnung gekommen, denn die Höhe h muss natürlich kürzer sein wie r, sonst könnte man ja gar kein Dreieck MAN zeichnen. Die Hypotenuse r ist schließlich im rechtwinkligen Dreieck immer die längste Seite. Daher muss die Kathete h kürzer sein als r.

Für die Definitionsmenge der Zielfunktion und der Ersatzzielfunktion gilt daher:

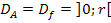
5. Schritt:Extrema der Ersatzzielfunktion 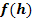berechnen

Hier noch einmal die Ersatzzielfunktion: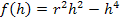

Wir bilden die erste Ableitung. Dabei ist zu beachten, dass nach h abgeleitet wird;r ist nur eine Konstante. Beim Ableiten nach h muss man sich nur auf die Potenzen von h konzentrieren.

Erste Ableitung: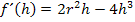

Die Ableitung setzten wir nun gleich Null und lösen dann nach h auf.

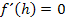
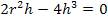
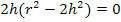
Ein Produkt ist bekanntlich gleich Null, wenn ein Faktor gleich Null ist. Daher kann man die Faktoren einzeln gleich Null setzen. Der erste Faktor 2h ist gleich Null, wenn h = 0 ist. Da h aber positiv sein muss, entfällt diese Lösung. Wir müssen nur den Ausdruck 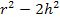gleich Null setzen und nach h auflösen.

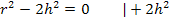
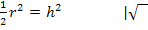
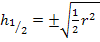
Wir radizieren das Ergebnis teilweise;d.h. wir ziehen soweit möglich einzeln die Wurzel. Das ergibt:

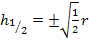
Nun machen wir noch den Nenner rational;d.h. wir formen so um, dass keine Wurzel mehr im Nenner steht. Endergebnisse sollten immer mit rationalem Nenner geschrieben werden. Daher erweitern wir mit 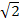. (Wenn du einen natural-display-Taschenrechner besitzt, kannst du das Nenner-rational-machen auch komplett mit dem Taschenrechner machen. Einfach 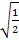in den Taschenrechner eingeben und auf die Ist-gleich-Taste drücken, dann erhältst du sofort das Ergebnis mit rationalem Nenner 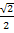.) Für die Schüler, die keinen solchen Taschenrechner zur Verfügung haben, werden im Folgenden die einzelnen Rechenschritte beim Nenner-rational-machen vorgeführt.

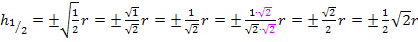
Wegen 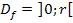kommt nur das positive Ergebnis in Frage;das negative Ergebnis liegt schließlich nicht innerhalb der Definitionsmenge. Es gibt somit nur ein einziges Extremum innerhalb der Definitionsmenge. Es liegt bei:

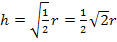
Art des Extremums überprüfen:

Wir verwenden die zweite Ableitung, um zu zeigen, dass an der Stelle 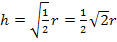ein Maximum vorliegt.

---