Was man an der Funktionsgleichung ohne lange Rechnung erkennen kann

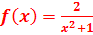
Die Funktion 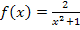hat keine Definitionslücken und daher keine senkrechten Asymptoten oder „Löcher“ (= stetig behebbare Definitionslücken). Es handelt sich um eine gebrochenrationale Funktion, deren Zählergrad kleiner als der Nennergrad ist. Deshalb ist die x-Achse die waagrechte Asymptote. Nullstellen hat 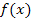keine, da ein Bruch nur dann gleich Null werden kann, wenn der Zähler gleich Null ist;der Zähler enthält hier aber gar kein x und kann somit nicht gleich Null werden. Da die Funktion nur eine gerade Potenz von x enthält, ist sie achsensymmetrisch zur y-Achse. Der Schnittpunkt mit der y-Achse lässt sich sehr leicht ermitteln, man muss nur für x Null einsetzen. Es ergibt sich: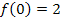

Der Schnittpunkt mit der y-Achse hat also die Koordinaten 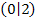. Auf Grund der Symmetrie muss es sich um einen Extrempunkt handeln. Da es keine Nullstellen gibt, die x-Achse waagrechte Asymptote ist und der Schnittpunkt mit der y-Achse oberhalb der x-Achse liegt, muss sich der Graph von oben an die x-Achse annähern.

So kommt man zu der Vermutung, dass der Schnittpunkt mit der y-Achse 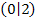der Hochpunkt des Graphen ist. (Es ist tatsächlich der einzige und somit absolute Hochpunkt von 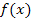. Das muss aber erst mit Hilfe der Ableitung nachgewiesen werden. Dazu ist dann doch eine kurze Rechnung nötig.)

Die Ableitung wird mit Hilfe der Quotientenregel gebildet.

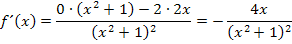
Damit ein Extremum vorliegen kann, muss gelten: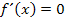

Die Ableitung 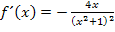wird nur an der Stelle 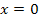gleich Null. Daher kann es keine weiteren Extrema geben. Überlegt man sich die Vorzeichen der Ableitung, stellt man fest, dass für die Monotonie von 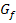gilt:

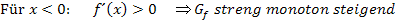
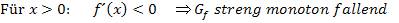
Oder in Tabellenform:

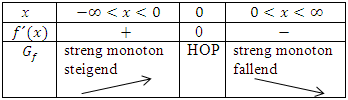
Es handelt sich also tatsächlich bei dem Schnittpunkt mit der y-Achse 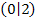um den einzigen Hochpunkt.

---