2. Berechnungen von Mittelwerten mit Hilfe von Integralen
Im Folgenden wird ausführlich die Berechnung der mittleren = durchschnittlichen Geschwindigkeit oder der mittleren Tagestemperatur erklärt.
Wie du weißt, entspricht das bestimmte Integral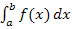 
der Fläche zwischen dem Graph der Funktion 
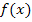und der x-Achse von x = a bis x = b. Das gilt zumindest dann, wenn der Graph von 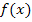oberhalb der x-Achse liegt und a kleiner als b ist;davon gehen wir nun aus. Was hat diese Fläche und somit auch das Integral mit der Berechnung eines Mittelwertes von 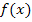zu tun? Das lässt sich am besten an der Berechnung der durchschnittlichen Geschwindigkeit, d.h. der mittleren Geschwindigkeit 
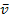erklären. (Der waagrechte Strich über dem v steht für Mittelwert von v. Das ist allgemein so gebräuchlich.)
Im Folgenden verwenden wir anstatt der Variablen x die Variable t und an Stelle von f die Funktionsbezeichnung v. Dabei steht wie üblich t für die Zeit (tempus = lat. Zeit) und v für die Geschwindigkeit, die ein Körper zum Zeitpunkt t hat (velocitas = lat. Geschwindigkeit, Schnelligkeit). Statt der x-Achse haben wir nun die t-Achse und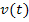 
ist eine Funktion in Abhängigkeit von der Zeit t. Außerdem nehmen wir statt a und b ab sofort 
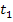und 
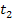als Integrationsgrenzen. Das Integral 
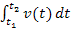entspricht dann der Fläche zwischen dem Graph der Funktion 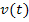und der t-Achse vom Zeitpunkt 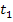bis zum Zeitpunkt 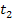. Diese Fläche entspricht wiederum der Strecke, die vom Zeitpunkt 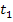bis zum Zeitpunkt 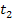zurückgelegt wurde. Um die innerhalb der Zeitspanne von 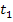bis 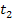zurückgelegte Strecke zu ermitteln, muss also das Integral 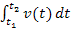berechnet werden. Die Zeit-Geschwindigkeits-Funktion 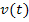ist dabei natürlich gegeben.
Strecke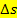 
, die durch einen Körper innerhalb der Zeitspanne von 
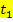bis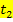 
zurückgelegt wurde:
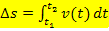
Warum das so ist, kann man sich am leichtesten erklären am Beispiel einer Bewegung mit konstanter Geschwindigkeit. Gehen wir beispielsweise von einem Auto aus, dass konstant mit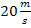 
geradeaus fährt. t steht nun für die Zeit in Sekunden ab Versuchsbeginn und v(t) für die Geschwindigkeit in 
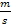zum jeweiligen Zeitpunkt t.
