2. Berechnungen von Mittelwerten mit Hilfe von Integralen

Es handelt sich um den Ausschnitt einer nach unten geöffneten Parabel mit Scheitel S(14|25). Weil 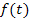offensichtlich eine quadratische Funktion ist, ist ihr Graph eine Parabel. Ihren Scheitel kannst du an der ursprünglich angegebenen Form 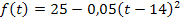direkt ablesen, weil es sich dabei im Prinzip um die Scheitelform der Parabel handelt;man braucht nur die Reihenfolge umzustellen. Aus der Funktionsgleichung 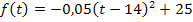lässt sich der Scheitel S(14|25) gut ablesen.

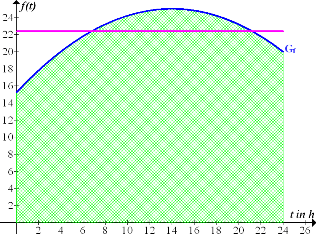
Abb.:Graph der Funktion 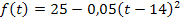in Blau und mittlere Tagestemperatur 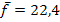in Rosa

Die gesamte grün schraffierte Fläche ist genauso großwie die rechteckige, rosa schraffierte Fläche unterhalb der waagrechten Gerade im Zeitintervall [0;24]. Betrachte dazu die nachfolgende Abbildung!

Zu 2b.)

Gesucht ist die mittlere Temperatur zwischen 8 Uhr und 18 Uhr. Daher gilt:

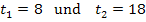
Die Berechnung geht fast genauso wie in Teilaufgabe 2a.) nur mit anderen Integrationsgrenzen.

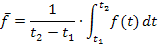
Statt der angegeben Funktion 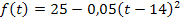verwenden wir die vereinfachte Form 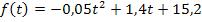, die wir in Teilaufgabe 2a.) schon ermittelt haben.

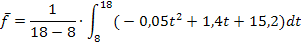
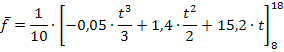
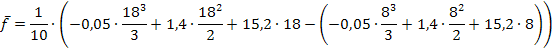
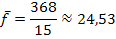
Die mittlere Temperatur zwischen 8 Uhr und 18 Uhr beträgt somit ungefähr 24,53 °C.

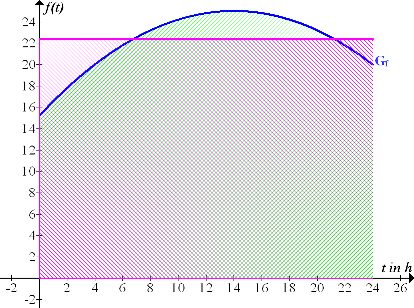
In der folgenden Abbildung sind die Zeit-Temperaturfunktion 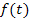und der Mittelwert der Temperatur 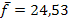zwischen 8 und 18 Uhr dargestellt. Die grün schraffierte Fläche unterhalb des blauen Graphen 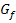entspricht dem Integral 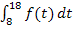;sie ist genauso großwie die rosa schraffierte, rechteckige Fläche unterhalb der rosafarbenen waagrechten Geraden.

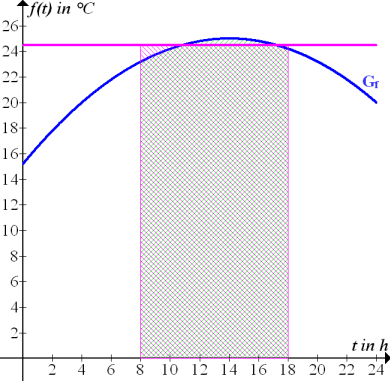
Abb.:Graph der Funktion 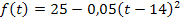in Blau und mittlere Temperatur zwischen 8 und 18 Uhr 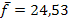in Rosa

3. Bsp.:

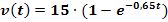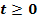Ein Körper fällt in einer bestimmten Flüssigkeit unter Reibungseinfluss senkrecht herunter. Mathematisch idealisiert lässt sich in Abhängigkeit von der Zeit t (in s) seine Geschwindigkeit v (in m/s) durch die Funktion für beschreiben.

a.) Welche Strecke hat der Körper innerhalb der ersten drei Sekunden durchfallen?

b.) Welche mittlere Geschwindigkeit 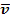hat der Körper innerhalb der ersten drei Sekunden?

c.) Welche mittlere Geschwindigkeit 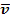hat der Körper zwischen der zweiten und fünften Sekunde?

Lösung:

Zu 3a.)

Gegeben ist die Zeit-Geschwindigkeitsfunktion 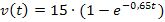für 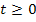. Gesucht ist die Strecke, die der Körper innerhalb der ersten drei Sekunden zurücklegt. Daher gilt:

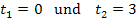
Der zurückgelegte Weg 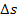entspricht der Fläche zwischen der Zeit-Geschwindigkeitsfunktion 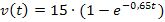und der t-Achse von .

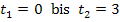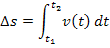
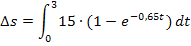
Nun müssen wir bloßnoch das Integral berechnen.

---