Die Integralfunktion und der HDI
h. einen Punkt mit waagrechter Tangente und Vorzeichenwechsel von 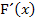 .
.
Wo der Graph von 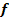 die x-Achse berührt, also nicht schneidet, d.h. wo
die x-Achse berührt, also nicht schneidet, d.h. wo 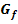 eine doppelte Nullstelle hat, besitzt der Graph von F einen Terrassenpunkt, d.h. einen Punkt mit waagrechter Tangente ohne Vorzeichenwechsel von
eine doppelte Nullstelle hat, besitzt der Graph von F einen Terrassenpunkt, d.h. einen Punkt mit waagrechter Tangente ohne Vorzeichenwechsel von 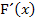 .
.
Die x-Koordinate der Nullstelle von f ergibt die x-Koordinate des Extremums bzw. Terrassenpunktes von F. Die y-Koordinate des Extremums / Terrassenpunktes von F entspricht natürlich nicht der y-Koordinate der Nullstelle von f, sondern der Flächenbilanz ausgehend von der unteren Grenze der Integralfunktion bis zum jeweiligen x-Wert.
Ist nur der Graph von f gegeben, kann die y-Koordinate eines Punktes von F nur grob geschätzt werden. Du versuchst dann die Flächenstücke oberhalb und unterhalb der x-Achse zu schätzen, indem du abzählst, wie viele Kästchen ungefähr hinein passen. Bei einem Maßstab von 1 cm auf beiden Achsen ergeben 4 Kästchen genau 1 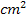 .
.
Vorsicht bei den Vorzeichen:Nur wenn du von links nach rechts also in die „richtige“ Richtung, integrierst, zählen Flächenstücke oberhalb der x-Achse positiv und die unterhalb der x-Achse negativ.
Integrierst du in die andere Richtung – du musst ja immer von der vorgegebenen unteren Grenze von F ausgehen – drehen sich die Vorzeichen entsprechend um!
Nun wenden wir die soeben erwähnten Zusammenhänge auf unser Aufgabenbeispiel an.
Hier noch einmal der Graph der Funktion f.
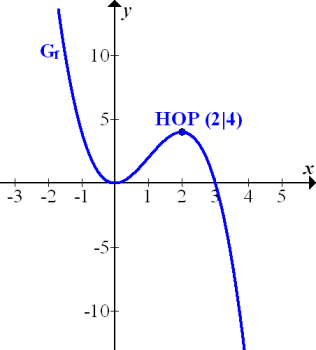
Abb.:Graph 
Wir lesen aus der Abbildung ab:Bei 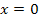 liegt eine doppelte Nullstelle von f vor;der Graph
liegt eine doppelte Nullstelle von f vor;der Graph  berührt schließlich im Ursprung die x-Achse. Bei
berührt schließlich im Ursprung die x-Achse. Bei 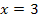 hat f eine einfache Nullstelle;der Graph
hat f eine einfache Nullstelle;der Graph  schneidet hier offensichtlich die x-Achse. Was lässt sich damit über den Graphen der Integralfunktion F sagen?
schneidet hier offensichtlich die x-Achse. Was lässt sich damit über den Graphen der Integralfunktion F sagen?
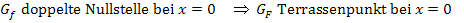
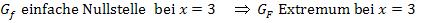
Nun muss die Art des Extremums von F bestimmt werden. Dazu untersuchen wir das Monotonieverhalten von F.
In der Abbildung des Graphen  erkennt man, dass
erkennt man, dass  für
für 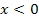 und für
und für 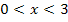 oberhalb der x-Achse verläuft.
oberhalb der x-Achse verläuft.
Für 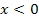 und
und 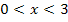 gilt:
gilt: 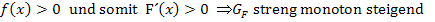
Außerdem sieht man, dass  für
für 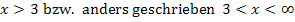 unterhalb der x-Achse verläuft.
unterhalb der x-Achse verläuft.
Für 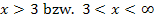 gilt:
gilt: 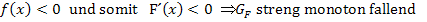
Wir fassen das alles in einer Monotonietabelle von F zusammen:
| x |  |
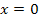 |
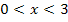 |
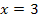 |
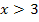 |
 |
oberhalb
der x-Achse |
doppelte Nst. | oberhalb
der x-Achse |
einfache Nst. | unterhalb
der x-Achse |
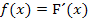 |
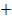 |
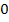 |
 |
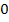 |
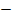 |
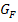 |
 steigt steigt |
TEP |  steigt steigt |
HOP |  fällt fällt |
Aus dem Steigungsverhalten von F wird klar, dass bei 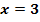 ein Hochpunkt von F vorliegt.
ein Hochpunkt von F vorliegt.

