Die Integralfunktion und der HDI
Nun fehlen noch die y-Koordinaten des Hochpunktes und des Terrassenpunktes.
Die y-Koordinate des Terrassenpunktes bei x = 0 kann exakt angegeben werden, denn wir haben bereits vorher festgestellt, dass im Ursprung eine Nullstelle von F vorliegt. Somit ist F(0) = 0 und der Terrassenpunkt ist TEP(0|0).
Die y-Koordinate des Hochpunktes bei x = 3 kann nur grob geschätzt werden. Es muss der Wert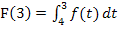 
ermittelt werden. Dieses Integral entspricht der Fläche zwischen 
und der x-Achse von x = 4 bis x = 3. Wir integrieren also in die „falsche“ Richtung. Die Fläche liegt unterhalb der x-Achse, zählt aber positiv auf Grund der umgekehrten Integrationsrichtung. Der Flächeninhalt ist schwer abzuschätzen. Am besten, du überlegst dir, wie viele Kästchen hineinpassen und teilst den Wert durch 4, denn 4 Kästchen haben zusammen einen Flächeninhalt von 1 
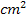. Das stimmt natürlich nur dann, wenn man die Funktion 
in einem Koordinatensystem mit dem Maßstab 1 LE = 1 cm gezeichnet hat. In diesem Fall schätzen wir die gesuchte Fläche auf circa 7 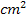. Daher gilt:
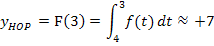
Der Hochpunkt von F hat die Koordinaten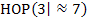 
.
Wendepunkte und Krümmungsverhalten von F:
Laut HDI gilt: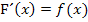 
und entsprechend auch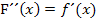 
Die Krümmung von F entspricht also der Steigung von f.
Um die Wendepunkte von F zu berechnen, muss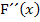 
gleich Null gesetzt werden, was dem Gleichnullsetzen von 
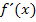entspricht. Wie du von der Kurvendiskussion einer Funktion weißt, ergeben sich aus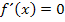 
die Punkte mit waagrechten Tangenten von f. Daraus folgt:F kann nur an denjenigen Stellen Wendepunkte haben, wo f Punkte mit waagrechten Tangenten besitzt. (Diesen Zusammenhang haben wir auch bei der Stammfunktion F schon kennengelernt. Siehe auch:Die Stammfunktion F(x) und einfache Integrationsregeln) Ein Wendepunkt von F liegt aber nur dann vor, wenn sich das Vorzeichen von 
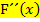bzw.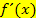 
ändert, d.h. wo f ein Extremum hat.
Zur Erinnerung:Es muss sich das Krümmungsverhalten einer Funktion ändern, damit wirklich ein Wendepunkt vorliegt. Ist zwar die Krümmung gleich Null, also die zweite Ableitung gleich Null, aber es liegt kein Vorzeichenwechsel der zweiten Ableitung vor, so handelt es sich nur um einen Flachpunkt und nicht um einen Wendepunkt der Funktion.
Zusammenhang des Verlaufs von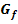 
mit dem Krümmungsverhalten von 
:
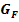In den Bereichen, wo der Graph 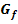streng monoton steigt, ist die erste Ableitung 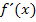positiv und somit auch die zweite Ableitung 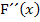positiv, d.h. der Graph der Integralfunktion 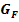ist dort linksgekrümmt.
