1. Flächenberechnungenmit Hilfe von Integralen

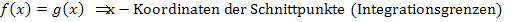
2. Schritt:Fläche zwischen und berechnen

Das weitere Vorgehen hängt von der Anzahl der Schnittpunkte von und ab.

·        Wenn es zwei Schnittpunkte gibt, welche die folgenden x-Koordinaten haben:

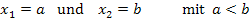
Für die Fläche zwischen und 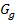gilt dann:

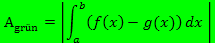
Der Betrag kann weggelassen werden, wenn a die kleinere und b entsprechend die größere Zahl ist und der Graph von die Fläche nach oben begrenzt.

Woher kommt die oben gezeigte Formel?

Wir gehen nun davon aus, dass der Graph 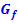die Fläche nach oben hin begrenzt und entsprechend der Graph 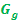die Fläche nach unten begrenzt, wie auch in den Abbildungen dargestellt. Zur Vereinfachung setzen wir voraus, dass beide Graphen im Bereich von a bis b oberhalb der x-Achse verlaufen. (Generell spielt es für die Fläche zwischen zwei Funktionen keine Rolle, ob die Funktionen oberhalb oder unterhalb der x-Achse liegen. Nur erklären lässt sich die Berechnung leichter, wenn die Graphen beider Funktionen oberhalb der x-Achse liegen.)

Leicht berechnen lässt sich mit dem Integral 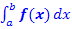diejenige Fläche, welche nur von 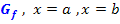und der x-Achse begrenzt wird. Wir bezeichnen diese Fläche mit .

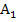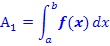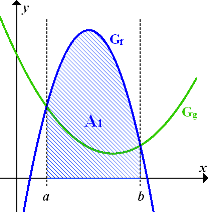
Abb.:Der Graph 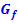und die Geraden x = a und x = b schließen mit der x-Achse die Fläche 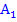ein.

Ebenso leicht lässt sich mit dem Integral 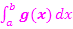diejenige Fläche berechnen, die von 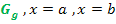und der x-Achse begrenzt wird. Wir bezeichnen diese Fläche mit .

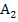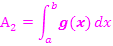Abb.:Der Graph 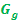und die Geraden x = a und x = b schließen mit der x-Achse die Fläche 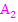ein.

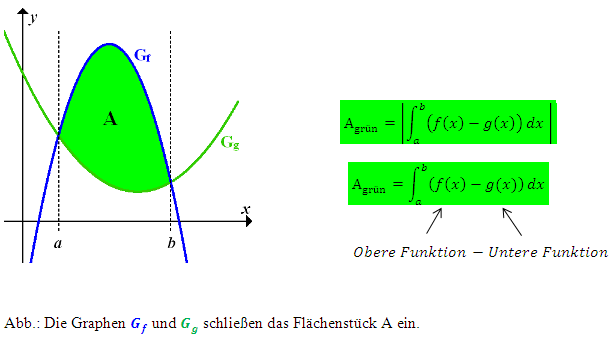
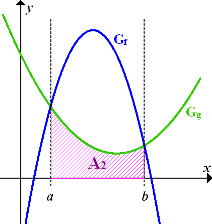
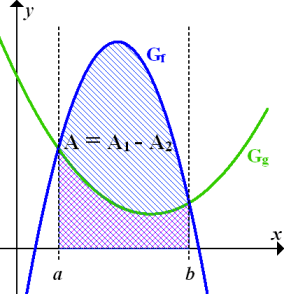
Um die Fläche A zwischen und 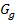(in der Abbildung ganz oben grün unterlegt;in der nachfolgenden Abbildung zur deutlicheren Darstellung einfach blau schraffiert) zu erhalten, muss nun von der Fläche 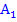die Fläche 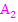abgezogen werden. (In der nachfolgenden Abbildung erscheint die Fläche 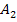lila, was daher kommt, dass die Rosa-Schraffierung von 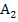durch die Blau-Schraffierung von 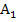überdeckt ist.) Die Fläche 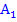zwischen und der x-Achse ist größer als die Fläche 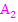zwischen 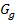und der x-Achse, weil im Bereich zwischen a und b oberhalb von 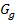verläuft. Deshalb muss ma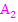n von 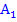subtrahieren, d.h.  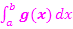  von 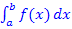abziehen.

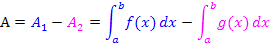Man kann die beiden Integrale zu einem einzigen Integral zusammenfassen, weil beide Integrale dieselben Grenzen haben.

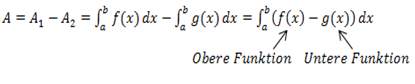
Um die Fläche A zwischen und 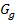zu ermitteln, muss das Integral 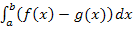berechnet werden. Die kleinere berechnete Abszisse a, also die x-Koordinate des linken Schnittpunkts, entspricht dabei der unteren Grenze des Integrals;die größere Abszisse b ist entsprechend die obere Grenze. Wir integrieren also von links nach rechts und der Graph von begrenzt die Fläche nach oben, entsprechend der Graph von 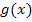nach unten.

---