1. Flächenberechnungenmit Hilfe von Integralen

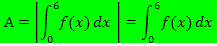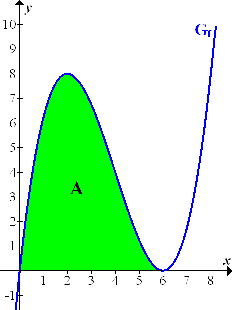
Abb.:Graph der Funktion 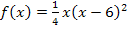mit der gesuchten Fläche A

Nun wissen wir, dass die gesuchte Fläche oberhalb der x-Achse liegt. Wir brauchen daher keinen Betrag um das Integral 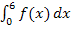zu setzen.

Berechnung der Fläche:

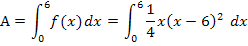
Damit wir 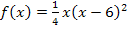leichter integrieren können, vereinfachen wir vorher den Funktionsterm, indem wir die Klammer auflösen. Zum Quadrieren der Klammer verwenden wir die zweite binomische Formel 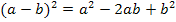. Danach kann das x in die Klammer hineinmultipliziert werden. Den Faktor 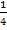multiplizieren wir besser nicht in die Klammer hinein. Dieser Faktor ist eine multiplikative Konstante, also eine Zahl ohne x, mit der multipliziert wird. Solche Konstanten bleiben beim Integrieren unverändert;man schreibt sie einfach ab. (Mehr dazu im Teil:Die Stammfunktion F(x) und einfache Integrationsregeln) Du kannst den Bruch auch in die Klammer hineinmultiplizieren und dann integrieren, aber dann musst du dich mit den dadurch entstehenden Brüchen herumplagen. Das wollen wir uns hier ersparen.

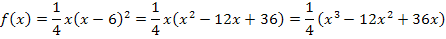
In dieser Form lässt sich bequem integrieren.

Dazu verwenden wir die Regel 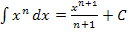. Weil es sich hier um ein bestimmtes Integral (Integral mit Grenzen) handelt, können wir  „+ C“ allerdings weglassen.

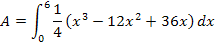
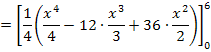
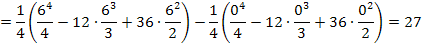
Die Fläche A zwischen und der x-Achse hat einen Flächeninhalt von 27 FE (Flächeneinheiten).

3. Bsp.:

Berechne das Integral 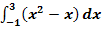und vergleiche das Ergebnis mit dem gesamten Flächeninhalt aller Flächenstücke, die durch den Graphen von 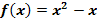, die Geraden x = -1 und x = 3 sowie durch die x-Achse begrenzt werden.

Lösung:

Berechnung des gesuchten Integrals:

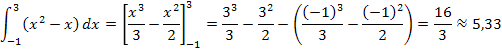
Berechnung des Gesamtflächeninhalts:

Wir müssen als erstes die Nullstellen von 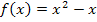berechnen, um festzustellen, ob eventuell eine oder mehrere der Nullstellen zwischen x = -1 und x = 3 liegen. Dort muss dann nämlich das Integral aufgeteilt werden.

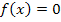
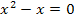
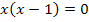
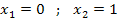
Beide Nullstellen liegen im Integrationsbereich. Um den gesamten Flächeninhalt aller Einzelflächen zu erhalten, müssen wir das Integral sowohl bei x = 0 als auch bei x = 1 aufteilen.

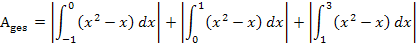
Der Betrag ist eigentlich nur bei dem mittleren Integral nötig, denn nur im Bereich 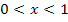liegt der Graph unterhalb der x-Achse. Das kannst du dir leicht vorstellen, denn ist eine nach oben geöffnete Normalparabel. (Die Funktion 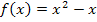ist schließlich eine Funktion der Form 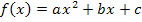mit a = 1;solche Funktionen beschreiben immer nach oben geöffnete Normalparabeln.) Nur das Integral 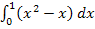wird daher einen negativen Wert liefern;die anderen beiden Integrale werden positive Ergebnisse haben. Man kann deshalb beim ersten und letzten Integral den Betrag auch weglassen. Betrachte dazu auch die folgende Abbildung!

---