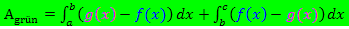1. Flächenberechnungenmit Hilfe von Integralen

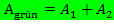
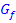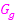Abb.:Die Graphen und schließen zwei Flächenstücke und 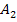ein. Der Gesamtflächeninhalt ist:

Es ist aber auch kein Problem, wenn man nicht weiß, welche jeweils die obere bzw. die untere Funktion ist. Dann zieht man einfach irgendeine der beiden Funktionen von der anderen ab, berechnet davon das Integral vom ersten Schnittpunkt zum zweiten Schnittpunkt und das Integral vom zweiten zum dritten Schnittpunkt usw. Dabei muss man allerdings den Betrag jedes der Einzelintegrale bilden. Die Beträge der einzelnen Integrale addiert, ergeben dann die gesamte Fläche zwischen den beiden Funktionen.

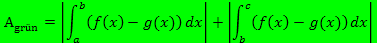
Gibt es noch weitere Schnittpunkte, integriert man entsprechend jeweils von einem zum nächstgrößeren Schnittpunkt;dann werden die Beträge der einzelnen Integrale alle addiert.

Nun genug zur Theorie, schauen wir uns doch endlich einige konkrete Beispiele für Flächenberechnungen mit Hilfe von Integralen an.

1. Bsp.:

Gegeben ist die Funktion .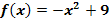

Berechne die Fläche, die von 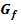, der x-Achse sowie den Geraden x = 1 und x = 2 begrenzt ist!

Lösung:

Vorweg fertigen wir uns eine Skizze an, die den Funktionsgraphen sowie die Geraden x = 1 und x = 2 enthält.

Bei 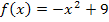handelt es sich um eine quadratische Funktion, also um eine Funktion der Form . Der Graph der Funktion 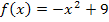ist eine nach unten geöffnete Normalparabel mit Scheitel bei S(0|9). Mehr dazu im Kapitel:Quadratische Funktionen (Parabeln)

Durch die Gleichungen x = 1 und x = 2 sind zwei im Koordinatensystem senkrecht verlaufende Geraden beschrieben. Die eine verläuft im Abstand 1 parallel zur y-Achse, die andere im Abstand 2.

Wenn man den Graph mit den senkrechten Geraden x = 1 und x = 2 in ein Koordinatensystem einzeichnet, erkennt man, dass die gesuchte Fläche komplett oberhalb der x-Achse liegt. Wir brauchen deshalb nachher keinen Betrag um das Integral zu setzen.

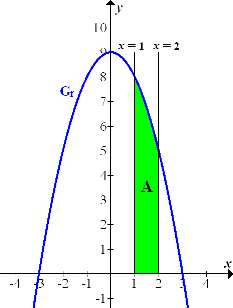
Abb.:Graph der Funktion 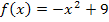mit der gesuchten Fläche A

Da die Funktion 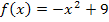offensichtlich keine Nullstellen zwischen x = 1 und x = 2 besitzt, können wir direkt von x = 1 bis x = 2 integrieren. (Die Funktion hat nur bei x = -3 und x = 3 Nullstellen;diese liegen aber nicht im Intervall von x = 1 bis x = 2. Wir brauchen daher das Integral nicht aufzuteilen.)

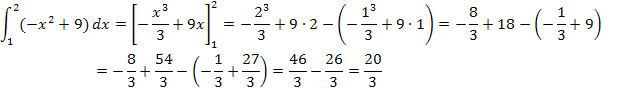
Die Fläche , die von 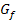, der x-Achse sowie den Geraden x = 1 und x = 2 begrenzt ist

2. Bsp.:

Berechne die Fläche, die durch den Graphen von 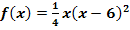und der x-Achse eingeschlossen wird!

Lösung:

Vorweg müssen wir die Integrationsgrenzen berechnen. Das sind die Nullstellen der Funktion 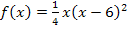. Bekanntlich werden die Nullstellen (Schnittpunkte mit der x-Achse) einer Funktion berechnet, indem man gleich Null setzt.

---