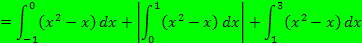1. Flächenberechnungenmit Hilfe von Integralen

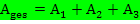
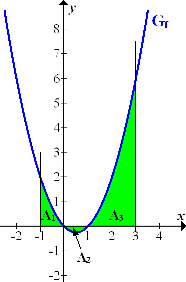
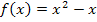Abb.:Der Graph der Funktion schließt mit der x-Achse und den Geraden x = -1 und x = 3 die Fläche 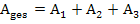ein.

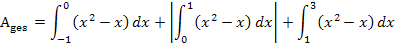
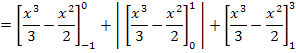
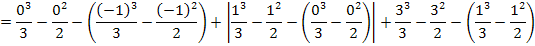
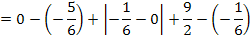
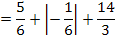
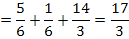
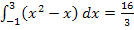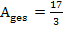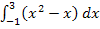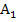Man erkennt, dass das Integral nicht den gleichen Wert hat wie . Das liegt daran, dass das Integral nur die Flächenbilanz ergibt. Die Flächenbilanz ist hier nicht dasselbe wie die der Inhalt der Fläche zwischen und der x-Achse von x = -1 bis x = 3, weil ein Teil der Fläche unterhalb der x-Achse liegt. Nur die Flächenstücke und 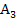liegen oberhalb der x-Achse und zählen bei der Flächenbilanz positiv. Das Flächenstück 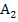liegt unterhalb der x-Achse und zählt bei der Flächenbilanz negativ.

Das Integral 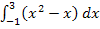setzt sich aus den folgenden Teilintegralen zusammen:

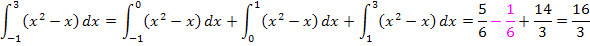
Das mittlere Integral liefert einen negativen Wert, da das zugehörige Flächenstück 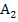unterhalb der x-Achse liegt. Daher geht es negativ in die Flächenbilanz ein.

Die gesamte Fläche wird aber folgendermaßen berechnet:

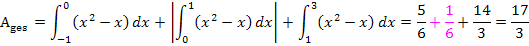
Bei der Berechnung der Gesamtfläche 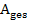muss der Betrag des mittleren Integrals gebildet werden, damit auch das Flächenstück 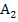, welches unterhalb der x-Achse liegt, positiv gezählt wird. (Ein Flächeninhalt kann schließlich nicht negativ sein, das Ergebnis eines Integrals dagegen schon.)

Man muss daher genau unterscheiden zwischen dem Integral 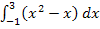, also der Flächenbilanz, und andererseits der Gesamtfläche aller Flächenstücke, aus denen sich das Integral zusammensetzt. Es hängt eben davon ab, was gefragt ist.

Achtung:Bitte die Aufgabenstellung genau lesen! Es ist wirklich ein riesiger Unterschied, ob einfach das Integral 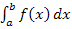gefragt ist, oder die Fläche zwischen 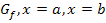und der x-Achse.

Ist wirklich das Integral 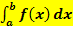gefragt, soll man direkt von a bis b integrieren, ohne das Integral aufzuteilen.

Ist dagegen nach der Fläche gefragt, muss das Integral gegebenenfalls bei den im Intervall [a;b] liegenden Nullstellen aufgeteilt und der Betrag der einzelnen Integrale gebildet werden, zumindest bei denjenigen Flächenstücken, die unterhalb der x-Achse liegen.

4. Bsp.:Fläche teilweise unterhalb und teilweise oberhalb der x-Achse

Gegeben ist die Funktion 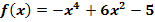mit 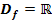. Berechne den gesamten Inhalt aller Flächenstücke, die von 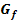und der x-Achse eingeschlossen werden.

Lösung:

Wir berechnen vorab die Nullstellen der Funktion 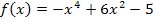, um die Integrationsgrenzen zu finden.

Nullstellenberechnung:

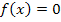
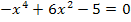
Dies ist eine Gleichung vierten Grades;d.h. eine Gleichung, bei der 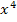die höchste auftretende Potenz der Unbekannten ist. Erfreulicherweise kommt aber weder 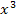noch 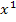in der Gleichung vor. Die Gleichung hat die Form 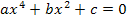und solche Gleichungen lassen sich bequem mit der folgenden Substitution lösen.

---