Das bestimmte und das unbestimmte Integral

Berechnung eines bestimmten Integrals:

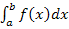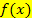Das bestimmte Integral wird berechnet, indem man zuerst die Stammfunktion der Funktion ermittelt. Auf die additive Konstante C kannst du beim bestimmten Integral verzichten, d.h. du darfst  „ + C “ weglassen. Die Stammfunktion schreibt man in eckige Klammern, wobei man an die rechte Klammer die Integrationsgrenzen schreibt. Dann setzt man in die Stammfunktion für jedes auftretende x einmal die obere Grenze b und einmal die untere Grenze a ein und zieht die Ergebnisse voneinander ab. Wichtig:Immer zuerst die obere Grenze eingesetzt minus die untere Grenze eingesetzt. (Nicht anders herum! Sonst wird das Vorzeichen des Integrals falsch.) Mathematisch geschrieben, sieht das Ganze folgendermaßen aus:

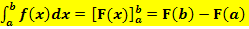
Sprich:„Integral von a bis b von f von x dx“

Schauen wir uns doch gleich ein paar konkrete Beispiele an. Dann verstehst du bestimmt, wie das gemeint ist.

1. Bsp.:

Berechne die folgenden bestimmten Integrale und deute die Ergebnisse jeweils geometrisch anschaulich mit Hilfe einer Skizze!

a.)

b.)

c.)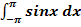

Lösung:

Bei den Teilaufgaben 1a.) und 1b.) wird die Stammfunktion mit der Integrationsformel 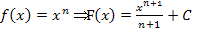ermittelt. (Bei einem bestimmten Integral darf allerdings die additive Konstante C weggelassen werden. Überlege dir doch gleich mal, warum man + C hier weglassen kann. Wenn du nicht selbst drauf kommst, keine Sorge:Die Antwort gibt´s etwas weiter unten.)

Zu 1a.)

Es ist das bestimmte Integral 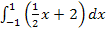zu berechnen und das Ergebnis geometrisch anschaulich zu deuten. Beginnen wir mit der geometrisch anschaulichen Deutung. Damit ist hier gemeint, dass man den Graph der Funktion 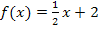in ein Koordinatensystem zeichnen soll und die Fläche zwischen und der x-Achse von 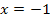bis 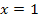markieren soll. Da die Fläche in diesem Beispiel komplett oberhalb der x-Achse liegt, entspricht der Flächeninhalt dieser Fläche genau dem gesuchten Integral. Vergleiche Abbildung!

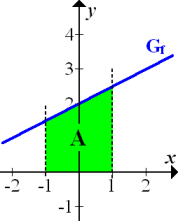
Abb.:Graph der Funktion 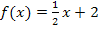mit der Fläche A, die dem gesuchten Integral 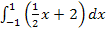entspricht

Nun aber endlich zur Berechnung des Integrals:

In einem ersten Schritt ermitteln wir eine Stammfunktion zu 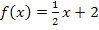. Damit du wirklich jeden Schritt verstehst, machen wir das extrem ausführlich, mit besonders vielen Zwischenschritten. Du musst natürlich nicht alle der folgenden Zwischenschritte hinschreiben, wenn du selbst rechnest. Im Gegenteil, du solltest versuchen mit möglichst wenigen Zwischenschritten zur Stammfunktion 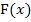zu kommen.

Wenn du die Stammfunktion gebildet hast, lässt du das Integralzeichen weg und setzt dafür eckige Klammern um die Stammfunktion 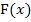herum. An die hintere Klammer schreibst du dabei die Integrationsgrenzen.

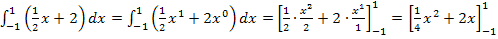
In einem weiteren Rechenschritt werden die Integrationsgrenzen in die Stammfunktion eingesetzt. Achte dabei auf die Reihenfolge beim Einsetzen der Grenzen! Es gilt immer:Obere Grenze eingesetzt minus untere Grenze eingesetzt!

Die obere Grenze ist immer diejenige Zahl, die oben am Integral steht. Die obere Grenze ist zwar meist größer als die untere. Das muss aber nicht immer so sein. Normalerweise integriert man zwar von links nach rechts (d.h. von der kleineren Zahl/untere Grenze zur größeren Zahl/obere Grenze). Es kann aber auch gelegentlich vorkommen, dass du ein Integral ausrechnen musst, bei dem die obere Grenze kleiner ist als die untere, also genau verkehrt herum. Wenn das Integral so angegeben ist, musst du trotzdem „obere Grenze minus untere“ rechnen:Obwohl die obere Grenze die kleinere Zahl ist, wird dennoch zuerst die obere Grenze eingesetzt und dann erst die untere eingesetzt und davon abgezogen.

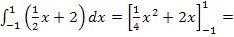
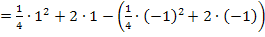
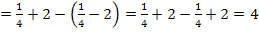
Die Fläche, die vom Funktionsgraph 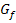, der x-Achse sowie den senkrechten Geraden 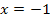und 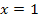begrenzt wird, hat einen Flächeninhalt von 4 FE (Flächeneinheiten). Du kannst dieses Ergebnis übrigens ganz leicht kontrollieren, indem du die Fläche elementargeometrisch berechnest. Das bedeutet, dass man die Fläche als Trapez oder zusammengesetzt aus Rechteck und Dreieck ansieht und mit Hilfe der Formeln für diese einfachen geometrischen Figuren die Fläche ausrechnet. Die elementargeometrische Berechnung der Fläche ist gerade zu Beginn der Integralrechnung oft neben der wirklichen Integration Teil der Aufgabe. Das kann natürlich nur dann verlangt werden, wenn die Fläche keine gebogenen Ränder hat, also nur bei Integralen von linearen Funktionen.

In diesem Fall ist die gesuchte Fläche ein Trapez mit den Grundlinien 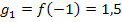und 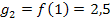. Das Trapez liegt quasi zur Seite gekippt vor uns. Die Höhe des Trapezes liegt auf der x-Achse. Da sie von -1 bis +1 geht, ist h = 2. Mit der Formel 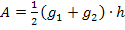für die Fläche eines Trapezes mit den Grundlinien 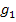und sowie der Höhe h, ergibt sich:

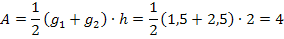
Dieses Ergebnis stimmt natürlich mit dem vorher berechneten Integral überein.

Das schwierigste bei der Berechnung eines bestimmten Integrals ist eigentlich die Ermittlung einer Stammfunktion 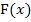zu . Je nach dem, wie die Funktionsgleichung von lautet, kann es nämlich ganz schön schwierig sein, eine Stammfunktion 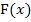zu finden.

---