Das bestimmte und das unbestimmte Integral
Deshalb ist die Formel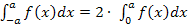 
wirklich sehr praktisch. Beim Einsetzen der Null als untere Grenze in die Stammfunktion ergibt sich oftmals insgesamt Null, so dass man viel weniger rechnen muss. Es sieht dann so aus, als hätte man das Einsetzen der Null einfach weggelassen.
Aber Vorsicht:Sobald z. B. ein Kosinus in der Stammfunktion vorkommt, darf man das Einsetzen der unteren Grenze 0 nicht einfach weglassen, denn es gilt: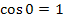 
Auch beim Einsetzen der Zahl 0 in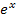 
muss man aufpassen, denn es gilt: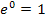 
Die beiden oben gezeigten Formeln zur Berechnung von bestimmten Integralen unter Ausnutzung der Symmetrie von f wollen wir nun gleich bei einigen konkreten Beispielen anwenden.
2. Bsp.:
Berechne die folgenden bestimmten Integrale, wenn möglich unter Ausnutzung der Symmetrie von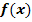 
!
a.)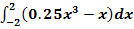 
b.)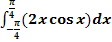 
c.)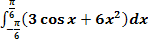 
d.) 
Lösung:
Bevor du hier jeweils versuchst eine Stammfunktion zu finden, solltest du erst einmal die Symmetrie von 
untersuchen, weil bei allen Integralen dieses Beispiels symmetrische Grenzen vorliegen. (Für die Zukunft:Immer wenn die Grenzen symmetrisch sind, also zum Beispiel -2 und +2 oder -4 und +4, erst die Symmetrie von untersuchen, bevor du versuchst das Integral auszurechnen, indem du eine Stammfunktion ermittelst und die Grenzen einsetzt.)
Zur Erinnerung:Die Symmetrie zum Koordinatensystem untersucht man, indem man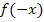 
bildet, d.h. man setzt für x in die Funktionsgleichung einfach 
ein, und schaut dann, ob man wieder auf kommt ( 
Achsensymmetrie zur y-Achse), oder ob man auf 
kommt ( Punktsymmetrie zum Ursprung)
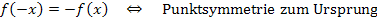
Bei einer Polynomfunktion kann man, wenn sie ausmultipliziert ist, die Symmetrie leicht erkennen:
Kommen nur gerade Potenzen von x vor, ist die Funktion achsensymmetrisch zur y-Achse. (Eine additive Konstante, d.h. Zahl ohne x, die addiert oder subtrahiert wird, gilt dabei als gerade Potenz.) Man bezeichnet solche Funktionen als gerade Funktionen.
Kommen nur ungerade Potenzen von x vor, ist die Funktion punktsymmetrisch zum Ursprung. Man bezeichnet solche Funktionen als ungerade Funktionen.
