Das bestimmte und das unbestimmte Integral
Das Produkt zweier achsensymmetrischer Funktionen ist wieder achsensymmetrisch;das gleiche gilt für den Quotienten zweier achsensymmetrischer Funktionen.
Das Produkt zweier punktsymmetrischer Funktionen ist dagegen achsensymmetrisch;das gleiche gilt für den Quotienten zweier punktsymmetrischer Funktionen.
Das Produkt einer achsensymmetrischen und einer punktsymmetrischen Funktion ist insgesamt punktsymmetrisch. Auch der Quotient einer achsensymmetrischen und einer punktsymmetrischen Funktion ist insgesamt punktsymmetrisch.
Das kannst du dir gut merken, wenn du bei einer zur y-Achse achsensymmetrischen Funktion an Plus denkst und bei einer zum Ursprung punktsymmetrischen Funktion an Minus. Mit den Vorzeichenregeln bei Mal und Geteilt kommt man leicht auf die Symmetrie eines Produkts oder eines Quotienten zweier symmetrischer Funktionen.
Plus mal Plus oder Plus durch Plus ergibt Plus.
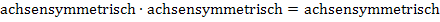
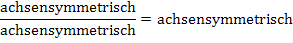
Minus mal Minus oder Minus durch Minus ergibt Plus.
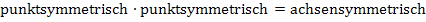
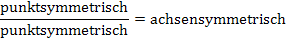
Minus mal Plus bzw. Plus mal Minus ist Minus. Ebenso Minus durch Plus bzw. umgekehrt Plus durch Minus ist Minus.
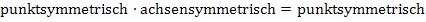
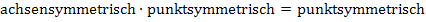
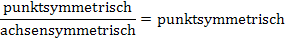
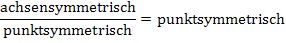
Merke dir außerdem, dass die Sinus-Funktion punktsymmetrisch zum Ursprung ist, die Kosinus-Funktion dagegen achsensymmetrisch zur y-Achse.
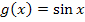
Symmetrie: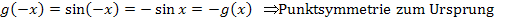 
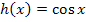
Symmetrie: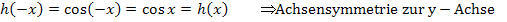 
Beim Kosinus fällt das Minus in der Klammer einfach weg, beim Sinus muss man das Minus in der Klammer nach vorne ziehen! Das ist für den rechnerischen Nachweis einer Symmetrie zum Koordinatensystem wichtig.
Nun wollen wir die soeben gewonnenen Erkenntnisse über die Symmetrie bei der Berechnung der gesuchten Integrale verwenden.
Zu 2a.)
Zu berechnen ist das Integral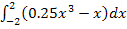 
.
Die Integrationsgrenzen sind symmetrisch. Mal sehen, wie es mit der Symmetrie der Integrandenfunktion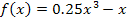 
aussieht.
Die Funktion hat nur ungerade Potenzen von x, ist also punktsymmetrisch zum Ursprung.
Rechnerischer Nachweis der Punktsymmetrie (zum Ursprung):
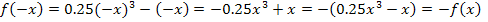
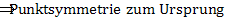
Wir können also den folgenden Zusammenhang ausnutzen:
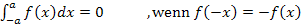
Daher gilt für das gesuchte Integral: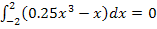 
Fertig!
Du kannst das Ergebnis aber auch noch selbst überprüfen, indem du das Integral „normal“ ausrechnest, d.h. eine Stammfunktion bildest und die Grenzen einsetzt:
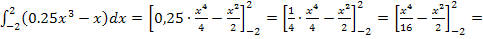
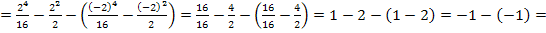
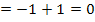
Wie erwartet kommt das Ergebnis 0 heraus. Dieses Integral hättest du also auch auf „normalem“ Weg berechnen können. Anders sieht das bei einigen der nächsten Teilaufgaben aus. Da wird es nämlich schwierig eine Stammfunktion zu finden. (Produkte und Quotienten darf man nicht einzeln Faktor für Faktor integrieren!
