Das Summenzeichen und die Streifenmethode
Wir denken uns die gesuchte Fläche A aufgeteilt in n Streifen gleicher Breite und berechnen sowohl die Obersumme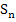 
als auch die Untersumme 
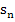. Je mehr man die Streifenanzahl n erhöht, desto mehr nähern sich Obersumme 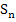und Untersumme 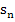an den exakten Inhalt der Fläche A an. Die Grenzwerte 
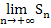und 
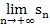führen dann letztendlich zum exakten Ergebnis von 
.
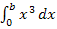Es gilt:
Untere Grenze a = 0, obere Grenze b und 
Anzahl der Streifen:n
Berechnung der Obersumme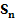 
:
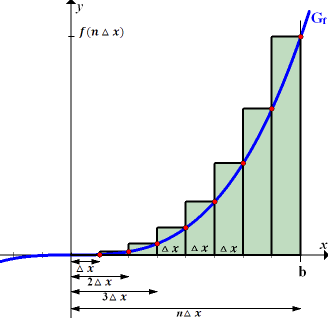
Abb. 12:Zur Berechnung der Obersumme 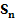im Intervall 0 bis b mit 
Hinweis:In Abb. 12 sind offensichtlich 8 Streifen dargestellt, doch musst du dir vorstellen, dass es sich allgemein um n Streifen handeln soll. Zu sehen ist in Abb. 12 also natürlich die Obersumme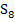 
. Leider lassen sich n Streifen nicht darstellen, ohne eine konkrete Zahl für n zu wählen. n = 8 ist nur als beliebiges Beispiel anzusehen. Betrachte den letzten Streifen am besten als den n.ten Streifen und nicht einfach als den achten!
Allgemeiner Ansatz für die Obersumme 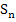für steigende Funktionen:
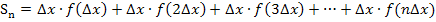
Wir klammern die Streifenbreite 
aus.
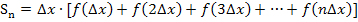
Für die Streifenbreite gilt:
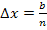
Damit ergibt sich für die Obersumme:
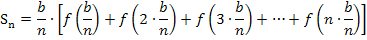
Anmerkung:Der Ausdruck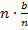 
wird absichtlich nicht gekürzt.
Damit du nachher leichter eine Gesetzmäßigkeit erkennen kannst, schreiben wir statt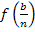 
ab sofort besser: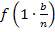 
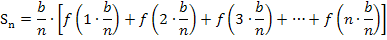
Auch dieser Ansatz gilt noch bei allen streng monoton steigenden Funktionen für die Obersumme. Ab jetzt werden wir aber konkret mit der Funktion rechnen.
Um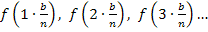 
bis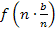 
zu ermitteln, setzen wir nun für x die Werte 
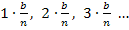bis 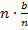in die gegebene Funktionsgleichung ein.
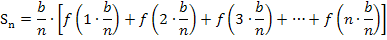
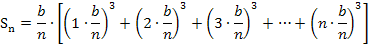
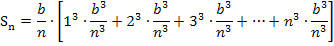
Jetzt müssen wir das Ganze soweit möglich vereinfachen. Wir klammern dazu zusätzlich zu 
auch noch den Faktor 
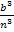aus. Das ergibt:
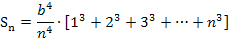
Den Ausdruck in der Klammer können wir mit dem Summenzeichen schreiben. In der Klammer steht nämlich die Summe der dritten Potenzen aller natürlichen Zahlen von 1 bis n. Weil wir die Potenzen vorher nicht ausgerechnet haben, ist das besonders gut zu erkennen.
Hier noch einmal die Formel für die Summe der dritten Potenzen:
Damit ergibt sich:
Als nächstes vereinfachen wir den entstandenen Term, indem wir mit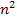 
kürzen und die Klammer mit der ersten binomischen Formel quadrieren. Statt durch 4 zu teilen, multiplizieren wir mit dem Kehrwert von 4, also mit 
. Dann sieht das Ganze schöner aus. Nach dem Kürzen mit 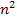verbleibt noch 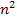im Nenner des ersten Bruchs. Dieses 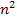schreiben wir besser in den Nenner des zweiten Bruchs. Dann lässt sich nachher leichter weiterrechnen.
