Scheitel und ein weiterer Kurvenpunkt gegeben
Jetzt hast du die Parabel in ihrer Scheitelform vorliegen und brauchst sie nur noch, wie oben bereits beschrieben, in die allgemeine Form 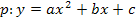 umwandeln.
umwandeln.
Bsp.: Die Parabel p hat den Scheitel S(-3|-4) und verläuft durch den Punkt A(-4|-3,5). Ermittle die Funktionsgleichung der Parabel p in der Form 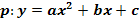 ! (
! (  )
)
Lösung:
Es wird im Folgenden der ausführliche Weg gewählt, d.h. es wird vorab nur der Scheitel in die Scheitelform eingesetzt und erst in einem zweiten Schritt auch der Kurvenpunkt A zusätzlich eingesetzt. (Natürlich könnten S und A auch gleichzeitig in die Scheitelform eingesetzt werden, doch wissen dann viele Schüler nicht, wie sie weiterrechnen müssen, wenn sie a ermittelt haben. Daher empfiehlt es sich eher, zuerst nur den Scheitel und erst im nächsten Schritt auch die Koordinaten von A in die Scheitelform einzusetzen.)
Scheitelform (allgemeiner Ansatz): 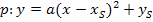
Scheitelkoordinaten einsetzen: 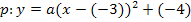
![]()

Kurvenpunkt einsetzen:![]()
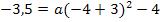
![]()
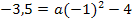
![]()
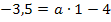
![]()
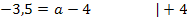
![]()
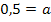
a in Gleichung * einsetzen:![]()

1. Binomische Formel anwenden: 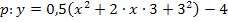
![]()
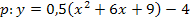
Ausmultiplizieren:![]()
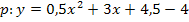
Zusammenfassen:![]()
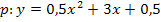
Nun ist die Gleichung der Parabel p in der gesuchten Form ermittelt.
| Zusammenfassung:
Gesucht: Gleichung einer Parabel mit gegebenen Scheitel · Scheitelform als allgemeiner Ansatz: · Die Scheitelkoordinaten für · Zusätzlich zum Scheitel jetzt auch die Koordinaten des Kurvenpunkts für x und y in die Scheitelform einsetzen · Nach a auflösen · Den soeben berechneten Wert für a in Gleichung * einsetzen · Scheitelform umrechnen in die allgemeine Form |
- Page 2 of 2
- « Previous
- 1
- 2
- Next »

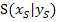 und einem bekannten Kurvenpunkt
und einem bekannten Kurvenpunkt und
und 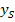 einsetzen (für x und y vorerst nichts einsetzen)
einsetzen (für x und y vorerst nichts einsetzen)  Gleichung *
Gleichung *