b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Rechnerisch lässt sich ausgehend von der Funktionsgleichung  die Funktionsgleichung einer Stammfunktion
die Funktionsgleichung einer Stammfunktion 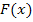 , abgesehen von der Konstante C, mit folgender Formel ermitteln:
, abgesehen von der Konstante C, mit folgender Formel ermitteln:
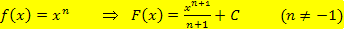
Bsp.:
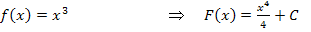
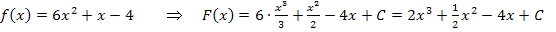
Weitere Beispiele und ausführlichere Erklärungen zur Ermittlung von Stammfunktionen findest du im Kapitel Einführung in die Integralrechnung.
Im nächsten Beispiel ist der Graph  gegeben und der Graph ihrer Ableitungsfunktion gesucht. Das ist also das umgekehrte Problem, wie gerade eben.
gegeben und der Graph ihrer Ableitungsfunktion gesucht. Das ist also das umgekehrte Problem, wie gerade eben.
3. Bsp.:
In der folgenden Abbildung ist der Graph 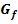 einer Funktion
einer Funktion 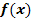 dargestellt. Skizziere den Verlauf des Graphen
dargestellt. Skizziere den Verlauf des Graphen 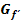 der zugehörigen Ableitungsfunktion! (Alle Hoch-, Tief- und Terrassenpunkte von
der zugehörigen Ableitungsfunktion! (Alle Hoch-, Tief- und Terrassenpunkte von 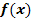 haben ganzzahlige x-Koordinaten;sie sind in der Abbildung rot markiert.)
haben ganzzahlige x-Koordinaten;sie sind in der Abbildung rot markiert.)
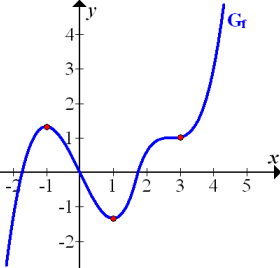
Wenn du die Aufgabe selbst lösen willst, solltest du dir Abbildung entweder vorher ausdrucken oder einfach abzeichnen!
Lösung:
Was wir hier machen sollen, kann man auch als „graphisches Differenzieren“ bezeichnen. Es ist keine Funktionsgleichung gegeben und es lässt sich, zumindest auf die Schnelle, keine Gleichung für  ermitteln. Wir sollen also direkt von
ermitteln. Wir sollen also direkt von  auf
auf  schließen
schließen
Du weißt hoffentlich:
Der Funktionswert y der Ableitungsfunktion entspricht der Tangentensteigung des Funktionsgraphen 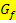 an dieser Stelle.
an dieser Stelle.
Will man beispielsweise für x = 0,5 den Funktionswert y der Ableitungsfunktion d.h. 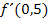 ermitteln, muss man bei x = 0,5 die Tangente an
ermitteln, muss man bei x = 0,5 die Tangente an  zeichnen und mit Hilfe eines Steigungsdreiecks die Tangentensteigung an dieser Stelle aus der Zeichnung ablesen. (Hast du Probleme, die Tangentensteigung aus der Zeichnung abzulesen? Dann gehe zu:Genauere Erklärung zum graphischen Differenzieren) Leider ist das meist eine recht ungenaue Sache, weil man erstens die Tangente nicht genau einzeichnen kann und zweitens sich die Steigung meist nur schlecht ablesen lässt. Aber eine andere Möglichkeit bleibt uns hier nicht.
zeichnen und mit Hilfe eines Steigungsdreiecks die Tangentensteigung an dieser Stelle aus der Zeichnung ablesen. (Hast du Probleme, die Tangentensteigung aus der Zeichnung abzulesen? Dann gehe zu:Genauere Erklärung zum graphischen Differenzieren) Leider ist das meist eine recht ungenaue Sache, weil man erstens die Tangente nicht genau einzeichnen kann und zweitens sich die Steigung meist nur schlecht ablesen lässt. Aber eine andere Möglichkeit bleibt uns hier nicht.
Um den Graph der Ableitungsfunktion zumindest grob skizzieren zu können, müssen wir als erstes diejenigen Punkte des Funktionsgraphen  suchen, wo die Steigung von
suchen, wo die Steigung von  eindeutig ablesbar ist. (Die Ableitung entspricht schließlich der Steigung von
eindeutig ablesbar ist. (Die Ableitung entspricht schließlich der Steigung von 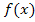 .) Am einfachsten ist dies bei Punkten mit waagrechten Tangenten:Dazu gehören die Extrema (Hoch- bzw. Tiefpunkte) und die Terrassenpunkte. Die x-Koordinaten dieser Kurvenpunkte lassen sich gut aus der Abbildung entnehmen, da laut Angabe alle Hoch-, Tief- und Terrassenpunkte ganzzahlige x-Koordinaten besitzen. Die Steigung von
.) Am einfachsten ist dies bei Punkten mit waagrechten Tangenten:Dazu gehören die Extrema (Hoch- bzw. Tiefpunkte) und die Terrassenpunkte. Die x-Koordinaten dieser Kurvenpunkte lassen sich gut aus der Abbildung entnehmen, da laut Angabe alle Hoch-, Tief- und Terrassenpunkte ganzzahlige x-Koordinaten besitzen. Die Steigung von  , also die Ableitung
, also die Ableitung  , ist an diesen Stellen gleich Null, weil die Tangente dort ja waagrecht verläuft.
, ist an diesen Stellen gleich Null, weil die Tangente dort ja waagrecht verläuft.

