Ausführliche Erklärung zum Auflösen von sgn im 3. Bsp.
Wie kann eine Funktion, deren Funktionsterm sgn enthält, ohne sgn schreiben? Wie schon gesagt, ordnet die Signum-Funktion jeder negativen Zahl den Wert -1 zu, jeder positiven Zahl den Wert +1. Der Zahl 0 wird durch die Signum-Funktion der Wert 0 zugeordnet. Daher kann die Funktion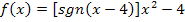 
folgendermaßen ohne sgn geschrieben werden:
Überlege dir, für welche Werte von x der Ausdruck, auf den sich sgn bezieht, negativ, positiv bzw. gleich Null wird.
Den Ausdruck, auf den sich sgn bezieht, nennt man übrigens das „Argument“ von sgn. Bei der Funktion 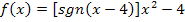ist das Argument von sgn also 
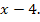Man muss sich dann überlegen, für welche Werte von x der Ausdruck 
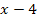negativ, positiv bzw. gleich Null wird. Der Ausdruck 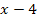ergibt Null für 
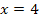. Ist x größer als 4, ist 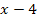positiv. Ist x dagegen kleiner als 4, ist 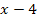negativ.
Wenn der Ausdruck 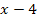negativ ist, also für 
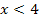, ersetzt man 
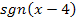einfach durch die Zahl -1.
Ist der Ausdruck 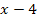gleich Null, also für 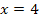, ersetzt man 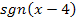einfach durch die Zahl 0.
Ist der Ausdruck 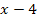positiv, also für 
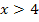, ersetzt man 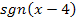einfach durch die Zahl +1.
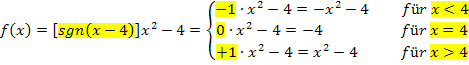
Nun ist dir hoffentlich klar geworden, wie man sgn auflöst.
