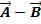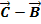Drei Punkte
1. Drei Punkte, die nicht auf einer Geraden liegen
Geg: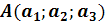 
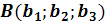
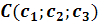
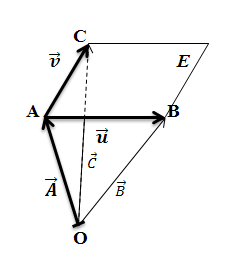
Als Aufpunkt der Ebene E kann ein beliebiger Ebenenpunkt verwendet werden. Die drei gegebenen Punkte A, B und C sollen alle in der Ebene E liegen. Daher können wir irgendeinen dieser drei Punkte verwenden. Wie meist üblich, nehmen wir den Punkt A als Aufpunkt. Wie in der Skizze gut zu erkennen ist, spannen die Vektoren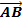 
und 
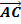die Ebene E auf, daher kann man diese Vektoren als Richtungsvektoren verwenden. Der erste Richtungsvektor 
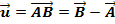und der zweite Richtungsvektor 
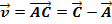werden nach der Regel „Spitze minus Fuß“ gebildet. (Es könnten an Stelle der Vektoren und auch beliebige Verbindungsvektoren der gegebenen Punkte als Richtungsvektoren verwendet werden, beispielsweise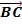 
und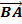 
.)
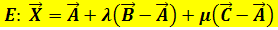
Bsp.: Ermittle drei verschiedene Gleichungen der Ebene E in Parameterform, welche die A(-2| 1| 5), B(3| 5|-1) und C(0| -7| 4) enthält!
Lösung:
Am einfachsten erhält man eine Parameterform der Ebene E, indem man in die Formel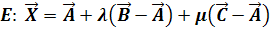 
einsetzt.
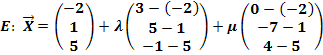
Am besten rechnest du den gerade gezeigten Zwischenschritt im Kopf;das spart Zeit. Aber Vorsicht mit den Vorzeichen! Hier passieren sehr oft Fehler! Du weißt: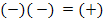 
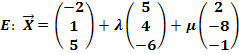
Eine andere Parametergleichung der Ebene E erhält man beispielsweise durch Verwendung eines anderen Aufpunkts (B oder C) oder durch Berechnung anderer Richtungsvektoren. Als Richtungsvektoren können alle Verbindungsvektoren der drei gegebenen Punkte verwendet werden.
Zweite Parametergleichung der Ebene E, mit Aufpunkt B(3|5|-1):
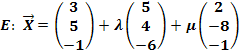
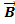
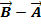
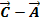
Dritte Parametergleichung der Ebene E, mit den Richtungsvektoren 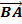und 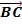:A(-2| 1| 5), B(3| 5|-1) und C(0| -7| 4)
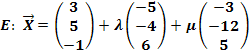
