1. Flächenberechnungenmit Hilfe von Integralen
Bei dem Graph der Funktion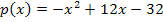 
handelt es sich um eine nach unten geöffnete Normalparabel. Wenn wir ihren Scheitel kennen, können wir sie zum Beispiel mit einer Parabelschablone bequem in das Koordinatensystem einzeichnen, das schon die Gerade enthält. Daher berechnen wir schnell die Koordinaten des Scheitelpunkts. (Zur Erinnerung:Der Scheitel ist nichts anderes als ein Extremum und wie man Extrema berechnet, weißt du bestimmt:Ableitung gleich Null setzen etc.)
Scheitelberechnung:
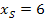
Nun kennen wir die x-Koordinate des Scheitels. Die y-Koordinate erhalten wir durch Einsetzen von 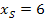in die Parabelgleichung.
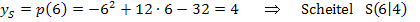
Jetzt können wir die Parabel 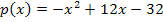und die Tangente 
gemeinsam in ein Koordinatensystem zeichnen.
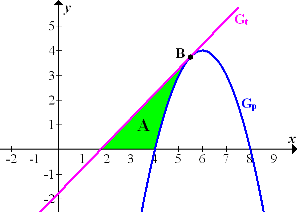
Abb. 1a) Die Graphen 
und 
derParabel 
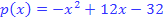und der Tangente 
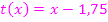schließen mit der x-Achse die Fläche A ein.
In Abb. 1a.) ist das gesuchte Flächenstück A grün markiert. Es ist oben durch die Gerade begrenzt. Unten ist es teils durch die x-Achse und teils durch die Parabel 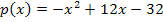begrenzt. Es handelt sich also weder um die Fläche zwischen einer Funktion und der x-Achse noch um die Fläche zwischen zwei Funktionen. Bisher haben wir besprochen, wie sich der Inhalt einer Fläche zwischen einer Funktion und der x-Achse oder zwischen zwei Funktionen berechnen lässt, wobei die Fläche links bzw. rechts durch senkrechte Geraden x = a und x = b begrenzt ist. Bei der gesuchten Fläche handelt es sich allerdings um eine Kombination aus einer Fläche zwischen Funktion und x-Achse mit einer Fläche zwischen zwei Funktionen. Wie kann man den Flächeninhalt A nun berechnen? Dafür gibt es zwei verschiedene Möglichkeiten.
1. Möglichkeit:
Wir teilen das Flächenstück A an der Stelle x = 4 (der linken Nullstelle der Parabel) auf. Wir berechnen dann erstens die Fläche zwischen Tangente und x-Achse von x = 1,75 (der Nullstelle der Tangente) bis zu x = 4 sowie zweitens die Fläche zwischen Tangente und Parabel von x = 4 bis zu x = 1.75 der x-Koordinate des Berührpunktes B beider Funktionen. Betrachte dazu Abb. 1b! (Die Nullstelle der Tangente, der Parabel und die x-Koordinate des Punktes B müssen wir jeweils noch ausrechnen.)
Jetzt das Ganze noch einmal ausführlich:
In Abb. 1b.) ist eine Fläche lila markiert;diese Fläche bezeichnen wir mit 
. Diese dreieckige Fläche ist die Fläche zwischen Tangente und x-Achse von der Nullstelle der Tangente x = 1,75 bis zur senkrechten Gerade x = 4.
Des Weiteren ist in Abb. 1b.) eine Fläche hellblau markiert;wir nennen sie im Folgenden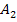 
. Dabei handelt es sich um die Fläche zwischen Tangente und Parabel von x = 4 bis zur x-Koordinate des Berührpunktes B.
