1. Flächenberechnungenmit Hilfe von Integralen
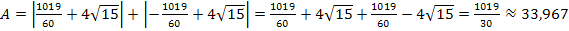
Der gesamte Inhalt der Fläche zwischen den Graphen  und
und  der beiden Funktionen
der beiden Funktionen 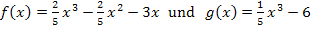 beträgt
beträgt 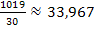 . Die Fläche setzt sich aus zwei Flächenstücken zusammen, wobei die größere der beiden einen Flächeninhalt von
. Die Fläche setzt sich aus zwei Flächenstücken zusammen, wobei die größere der beiden einen Flächeninhalt von 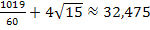 besitzt und die kleinere einen Inhalt von
besitzt und die kleinere einen Inhalt von 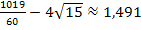 . Betrachte dazu die folgende Abbildung!
. Betrachte dazu die folgende Abbildung!
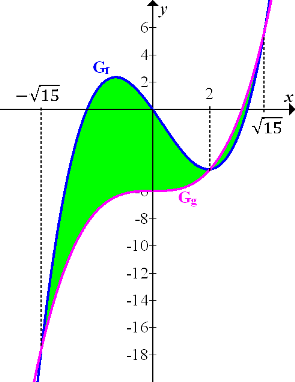
Abb.:Die Graphen 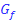 und
und 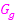 der Funktionen
der Funktionen 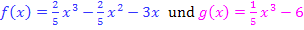 schließen zwei Flächenstücke ein.
schließen zwei Flächenstücke ein.
An dieser Teilaufgabe konntest du sehen, dass sich die Fläche zwischen zwei Funktionen auch dann relativ einfach berechnen lässt, wenn man sich den Verlauf der Graphen nicht vorstellen kann. Die soeben gezeigte Abbildung war für die vorherige Berechnung der Fläche nicht notwendig. Die Abbildung soll dir allerdings nachträglich zeigen, wie die Flächenstücke liegen, deren gemeinsamen Inhalt wir vorher berechnet haben.
8. Bsp.:Fläche zwischen einer Funktion und einer Funktionenschar
Die Graphen der Funktionen 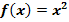 und
und 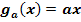 mit a
mit a  ℝ {0} schließen ein Flächenstück ein.
ℝ {0} schließen ein Flächenstück ein.
a.) Berechne den Inhalt dieser Fläche in Abhängigkeit von a.
b.) Für welche Werte von a mit a  ℝ {0} hat dieses Flächenstück den Inhalt 36?
ℝ {0} hat dieses Flächenstück den Inhalt 36?
Lösung:
Zu 8a.)
Hier ist die Fläche zwischen zwei Funktionsgraphen (in Abhängigkeit von a) gesucht, nicht die Fläche zwischen einer Funktion und der x-Achse. Daher müssen wir die x-Koordinaten der Schnittpunkte beider Funktionen ermitteln und nicht die Nullstellen der beiden Funktionen. (Die Nullstellen von  und
und 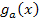 sind für die Fläche zwischen den beiden Graphen unwichtig.)
sind für die Fläche zwischen den beiden Graphen unwichtig.)
Berechnung der x-Koordinaten der Schnittpunkte von 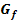 und
und 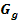 in Abhängigkeit von a
in Abhängigkeit von a
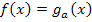

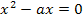
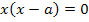
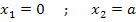
Laut Angabe gilt a  ℝ {0}. Daher kann a nicht gleich Null sein. Es existieren hier also immer zwei verschiedene Schnittpunkte, weil für a
ℝ {0}. Daher kann a nicht gleich Null sein. Es existieren hier also immer zwei verschiedene Schnittpunkte, weil für a  ℝ {0} die zweite Lösung
ℝ {0} die zweite Lösung 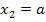 nicht mit der ersten Lösung
nicht mit der ersten Lösung 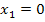 zusammenfallen kann. Die beiden Funktionen schneiden sich für a
zusammenfallen kann. Die beiden Funktionen schneiden sich für a  ℝ {0} immer genau zweimal.
ℝ {0} immer genau zweimal.
Wir kennen somit die beiden Integrationsgrenzen: 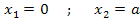
Das Problem ist jedoch, dass wir nicht sagen können, welche die kleinere und welche die größere Zahl ist, ob also a kleiner oder größer ist als 0. Das hängt nämlich vom Vorzeichen von a ab. Für a >0 ist a größer als die Zahl 0, weil a dann wirklich für eine positive Zahl steht. Aber für a <0 ist es genau umgekehrt, weil a dann selbst für eine negative Zahl steht und – a entsprechend für eine Positive stehen würde. Also ist für a <0 der Parameter a kleiner als die Zahl 0. Es ist somit für a  ℝ {0} allgemein nicht möglich zu sagen, welche der beiden Grenzen 0 und a die Kleinere bzw. die Größere ist. Weil wir das nicht eindeutig sagen können und wir deswegen keine Fallunterscheidung machen wollen, muss der Betrag des Integrals verwendet werden. Mit dem Betrag ist es egal, welche der beiden Schnittstellen die obere bzw. untere Grenze ist. Wir wählen 0 als untere Grenze, da es sich damit besser rechnen lässt.
ℝ {0} allgemein nicht möglich zu sagen, welche der beiden Grenzen 0 und a die Kleinere bzw. die Größere ist. Weil wir das nicht eindeutig sagen können und wir deswegen keine Fallunterscheidung machen wollen, muss der Betrag des Integrals verwendet werden. Mit dem Betrag ist es egal, welche der beiden Schnittstellen die obere bzw. untere Grenze ist. Wir wählen 0 als untere Grenze, da es sich damit besser rechnen lässt.

